21. 解析：本题需要把实际问题转化为数学模型，构造直角三角形，利用勾股定理完成.

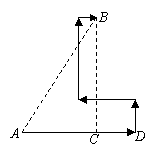答案：如图，过点B作BC⊥AD于C，则AC=2.5，BC=6，

由勾股定理求得AB=6.5(km) .

所以登陆点A与宝藏埋藏点B之间的距离是6.5km.

20. 解析：①只须画直角边为2和3的直角三角形即可.这时直角三角形的面积为：

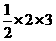=3；②画面积为5的四边形，我们可画边长的平方为5的正方形即可.

答案：如图1和图2.

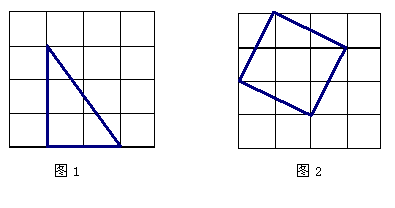
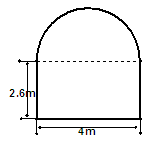
19. 解析：如图，卡车能否通过，关键是车高4米与AC的比较，BC为2.6米，只需求AB，在直角三角形OAB中，半径OA为2米，车宽的一半为DC = OB =1.4米，运用勾股定理求出AB即可.

答案：过直径的中点O，作直径的垂线交下底边于点D，

如图所示，在Rt△ABO中，由题意知OA=2，DC = OB =1.4，

所以.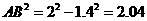

因为4－2.6=1.4,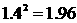，2.04>1.96,所以卡车可以通过.

答：卡车可以通过，但要小心.

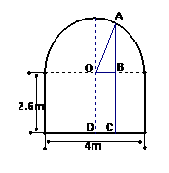
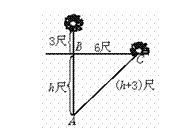
18．解析：本题关键是能将红莲移动后的图画出, 红莲被吹至一边，花朵刚好齐及水面即AC为红莲的长.

答案：设水深为h尺.如图，Rt△ABC中，AB=h，AC=h+3，BC=6，

由勾股定理得：AC²=AB²+BC²，即(h+3)²=h²+6².

∴h²+6h+9=h²+36，解得：h=4.5.

答：水深4.5尺.

17．解析：找最短路程，只需要找到A点关于河岸的对称点和点B的距离就可以，借助勾股定理可以求出来.

答案：如图，作出A点关于MN的对称点A′，连接A′B交MN于点P，则A′B就是最短路线. 在Rt△A′DB中，由勾股定理求得A′B=17km.

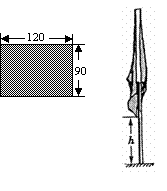
16．解析：如图14，彩旗下垂时最低处离地面的最小高度h也就是旗杆的高度减去彩旗的对角线的长，彩旗的对角线长为150，所以h=320-150=170cm.

答案：彩旗下垂时最低处离地面的最小高度h为170cm.．

15.解析：本题是一道古代数学题，由于树可以近似看作圆柱，藤条绕树缠绕，我们可以按图的方法，转化为平面图形来解决．如图13,线段AB的长就是古藤的长.

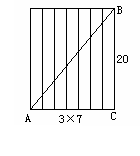答案：如图13，在Rt△ABC中，由勾股定理得

AB²=BC²+AC².

因为BC=20，AC=3×7=21，

所以AB²=20²+21²=841.

所以AB=29.

所以这根藤条有29尺．

答：这根藤条有29尺．

14．解析：如图，把实际问题转化为数学模型，构造直角三角形，然后利用勾股定理解决．

答案：在Rt△ABC中，AB²+BC²=AC²，所以AB²+140²=500²，解得AB=480．

答：该河AB处的宽度为480米．

13．解析：三级台阶平面展开图为长方形，长为2，宽为(0.2+0.3)×3则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长．可设蚂蚁沿台阶面爬行到B点最短路程为x ，由勾股定理得：x²＝2²+[(0.2+0.3)×3]²=2.5² ，x＝2.5．

答案：2.5．

12．解析：如图9，把实际问题转化为数学模型，构造直角三角形，然后利用勾股定理解决．设树的高度为x米， 因两只猴子所经过的距离相等都为30米．由勾股定理得：x²+20²=[30-(x-10)]²，解得x=15．

答案：15．