
题目列表(包括答案和解析)
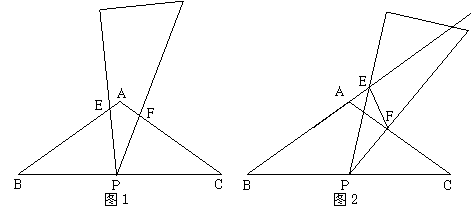
27、等腰△ABC,AB=AC,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.
(1)如图1,当三角板的两边分别交AB、AC于点E、F时.说明:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图2情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
① 探究1:△BPE与△CFP还相似吗?(只需写出结论)
② 探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
(3) 将三角板绕点P旋转的过程中,三角板的两边所在的直线分别与直线AB、AC于点E、F.
① △PEF是否能成为等腰三角形?若能,求出△PEF为等腰三角形时∠BPE的度数;若不能,请说明理由.
② 设BC=8,EF=m,△EPF的面积为S,试用m的代数式表示S.
26、(1)探究新知:
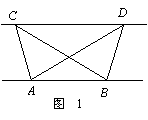 如图1,已知△ABC与△ABD的面积相等,
如图1,已知△ABC与△ABD的面积相等,
试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
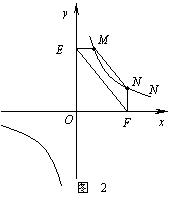 ① 如图2,点M,N在反比例函数
① 如图2,点M,N在反比例函数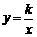 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.
试证明:MN∥EF.
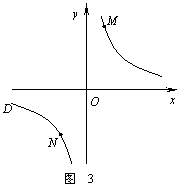
② 若①中的其他条件不变,只改变点M,N
的位置如图3所示,请判断 MN与EF是否平行.
(请画出图形,并简要说明你判断的理由.)

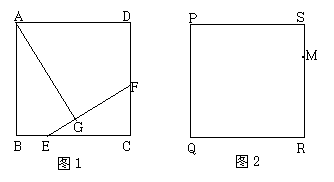
25、(1)如图1,E、F分别是正方形ABCD的边BC、CD上一点,AG⊥EF于G,若AG=AB,
证明:EF=BE+DF
(2)如图2,M是正方形PQRS的边SR上一点,在边RQ上求作一点N,使得MN=SM+QN(不写作法,保留作图痕迹,不要求证明).
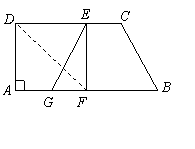
24、如图,在直角梯形纸片 中,
中, ,
, ,
,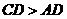 ,将纸片沿过点
,将纸片沿过点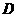 的直线折叠,使点
的直线折叠,使点 落在边
落在边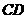 上的点
上的点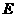 处,折痕为
处,折痕为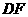 .连接
.连接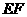 并展开纸片.
并展开纸片.
(1)求证:四边形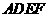 是正方形;
是正方形;
(2)取线段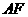 的中点
的中点 ,连接
,连接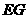 ,如果
,如果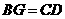 ,试证明四边形
,试证明四边形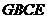 是等腰梯形.
是等腰梯形.
23、小华与小丽设计了 两种游戏:
两种游戏:
游戏 的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
游戏 的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
22、已知正比例函数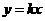 的图象与反比例函数
的图象与反比例函数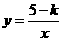 (
(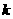 为常数,
为常数,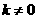 )的图象有一个交点的横坐标是2.
)的图象有一个交点的横坐标是2.
(1)求两个函数图象的交点坐标;
(2)若点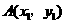 ,
,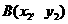 是反比例函数
是反比例函数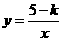 图象上的两点,且
图象上的两点,且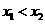 ,试比较
,试比较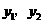 的大小.
的大小.
21、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF。
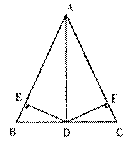 (1)图中有几对全等的三角形?请一一列出;
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明。
20、已知分式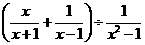 ,及一组数据:
,及一组数据: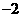 ,
,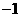 ,1,2.
,1,2.
(1)从已知数据中随机选取一个数代替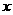 ,能使已知分式有意义的概率是多少?
,能使已知分式有意义的概率是多少?
(2)先将已知分式化简,再从已知数据中选取一个你喜欢的,且使已知分式有意义的数代替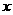 求值.
求值.
19、(1)请从下列三个代数式中任选两个构成一个分式,并化简该分式
x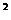 -4xy+4y
-4xy+4y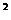 x
x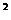 -4y
-4y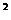 x-2y
x-2y
(2)解方程 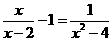
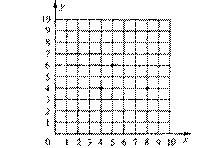
18、如图,在方格棋盘上有三枚棋子,位置分别为(4,4),(8,4),(5,6)。请你再放下一枚棋子,使这四枚棋子组成一个平行四边形,这枚棋子的坐标可以是_____________________________.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com