
题目列表(包括答案和解析)
3.解:
(1)过点A作AD⊥BC于D,则有AD=3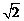 ×sin450=
×sin450=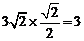 .
.
设△MNC的MN边上的高为h,
∵MN∥BC,∴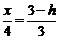 .
.
∴h=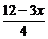 ,
,
∴S=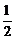 MN·h=
MN·h=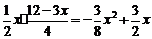 ,
,
即S=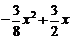 (0<x<4).
(0<x<4).
(2)若存在这样的线段MN,使S△MNC=2,则方程 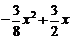 =2必有实根,
=2必有实根,
即3x2-12x+16=0 必有实根.
但△=(-12)2-4×3×16=-48<0,说明此方程无实根,
所以不存在这样的线段MN.
2.解:(1)∵OA=OB,AB=AC,∴△AOB和△ABC是等腰三角形.
∴∠B=∠BAO=∠C.∴△AOB∽△BAC.
∴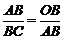 , 即
, 即 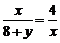 ,
,
∴y=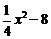
∵A为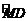 上任意一点,BM≤AB≤BD,
上任意一点,BM≤AB≤BD,
而BM=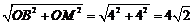 , BD=8,
, BD=8,
∴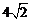 ≤x≤8.
≤x≤8.
∴y=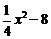 (
(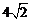 ≤x≤8).
≤x≤8).
(2)若OA⊥CA,则AC为⊙O的切线,即当OC2=OA2+AC2时,OA⊥CA,
∴(4+y)2=42+ x2,即y2+8y=x2.
由y=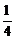 x2-8和y2+8y=x2两式可得y=4,
x2-8和y2+8y=x2两式可得y=4,
∴x=4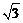 ,即当x=4
,即当x=4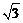 时,CA是⊙O的切线.
时,CA是⊙O的切线.
(3)由(2)得x=4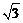 ,CA是⊙O的切线,
,CA是⊙O的切线,
此时y=4,
而OE=BE-OB=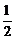 (8+4)-4=2,AE=
(8+4)-4=2,AE=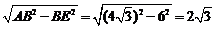 ,
,
∴tan∠OAE=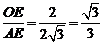 .
.
(2)z=y·x-40y-500-1500
=(30-0.1x)x-40(30-0.1x)-2000
=30x-0.1x2-1200+4x-2000
=-0.1x2+34x-3200.
(3)当x=160时,z=-0.1x2+34x-3200=-0.1×1602+34×160-3200=-320.
把z=- 320代入z=-0.1x2+34x-3200,
得-320=-0.1x2+34x-3200,x2-340x+28800=0,
∴(x-160) (x-180)=0.∴x=160或x=180.
当x=160时,y=-0.1x+30=-0.1×160+30=14(万件);
当x=180时,y=-0.1x+30=-0.1×180+30=12(万件).
∴S=x(6-x)=-x2+6x,即S=-x2+6x,其中0<x<6.
(2)设此黄金矩形的长为x米,宽为y米,
则由题意,得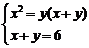 ,解得
,解得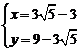
即当把矩形的长设计为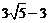 米时,矩形将成为黄金矩形,
米时,矩形将成为黄金矩形,
此时S=xy=(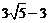 )(
)(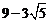 )=
)=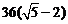 ;
;
可获得的设计费为 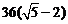 ×1000≈8498(元).
×1000≈8498(元).
12.解:(1)当t=5时,y=195,当t=25时,y=205.
∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.
(2)当0<t≤10时,y=-t2+24t+100=-(t-12)2+244,
该图的对称轴为t=12, 在对称轴左侧,y随x的增大而增大,
所以,当t=10时,y有最大值240.
当10<t≤20时,y=240.
当20<t≤40时,y=-7t+380,y随x的增大而减小,
故此时y<240.
所以,当t=20时,y 有最大值240.
所以,讲课开始后10分钟时,学生的注意力最集中,能持续10分钟.
(3)当0<t≤10,令y=-t2+24t+100=180,
∴t=4.
当20<t≤40时,令=-7t+380=180,
∴t=28.57.
所以,老师可以经过适当安排,能在学生注意力达到所需的状态下讲解完这道题目.
二次函数C卷答案:
(二)10.解:如答图,S矩形PNDM=xy,且2≤x≤4.
延长NP交EF于G,显然PG∥BF.
故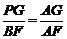 ,即
,即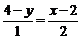 ,∴y=-
,∴y=-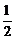 x+5,
x+5,
∴S=xy=-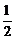 x2+5x,即S=-
x2+5x,即S=-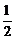 x2+5x(2≤x≤4).
x2+5x(2≤x≤4).
9.解:把x=3,y=15;x=-2,y=5分别代入y=ax2+(xm+c),
得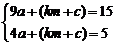
解得a=2,km+c=-3, ∴y=2x2-3.
8.解:(1)由图象可知,当x=600时,y=400;当x=700时,y=300,
代入y=kx+b中,得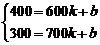
解得k=-1,b=1000
∴y=-x+1000(500≤x≤800)
(2)销售总价=销售单价×销售量=xy,成本总价=成本单价×销售量=500y,
代入毛利润公式,得
S=xy-500y=x(-x+1000)-500(-x+1000)
=-x2+1500x-500000.
∴S=-x2+1500x-500000(500≤x≤800)
7.解:由题意,得每件商品的销售利润为(x-30)元,那么m件的销售利润为y=m(x-30).
又∵m=162-3x,∴y=(x-30)(162-3x),
即y=-3x2+252x-4860.
∵x-30≥0,∴x≥30.
又∴m≥0,∴162-3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=-3x2+252x-4860(30≤x≤54).
6.解:若销售单价为x元,则每千克降低(70-x)元,日均多销售出2(70-x)千克,日均销售量为[60+2(70-x)]千克,每千克获利(x-30)元.依题意,得
y=(x-30)[60+2(70-x)]-500
=-2x2+260x-6500(30≤x≤70).
即y=-2x2+260x-6500(30≤x≤70).
5.解:∵PB=6-t,BE+EQ=6+t,
∴S=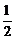 PB·BQ=
PB·BQ=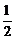 PB·(BE+EQ)
PB·(BE+EQ)
= 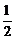 (6-t)(6+t)=-
(6-t)(6+t)=-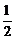 t2+18.
t2+18.
∴S=-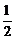 t2+18(0≤t≤6).
t2+18(0≤t≤6).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com