
题目列表(包括答案和解析)
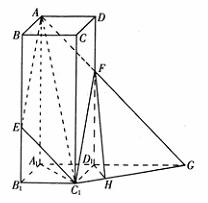
12. 如图(上右图),在正四棱柱
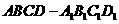 中,
中,
 ,
, 为
为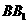 上使
上使 的点。平面
的点。平面 交
交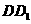 于
于 ,交
,交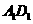 的延长线于
的延长线于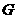 ,求:
,求:
(Ⅰ)异面直线 与
与 所成角的大小;
所成角的大小;
(Ⅱ)二面角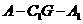 的正切值;
的正切值;
 [解] 解法一:(Ⅰ)由
[解] 解法一:(Ⅰ)由 为异面直线
为异面直线 所成的角。连接
所成的角。连接 .因为AE和
.因为AE和 分别是平行平面
分别是平行平面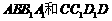 与平面
与平面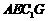 的交线,所以
的交线,所以 ,由此可得
,由此可得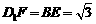 ,再由
,再由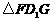 ∽
∽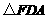 得
得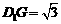
在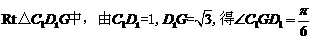 。
。
(Ⅱ)作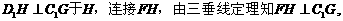
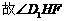 为二面角
为二面角 即二面角
即二面角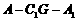 的平面角
的平面角
在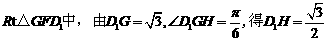 ,
,
从而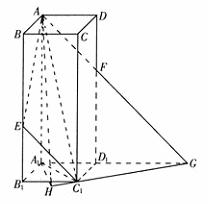
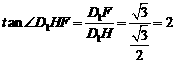
解法二:(Ⅰ)由 为异面直线
为异面直线
 所成的角。因为
所成的角。因为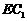 和
和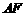 分别是平行平面
分别是平行平面 与平面
与平面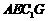 的交线,
的交线,
所以 ,由此可得
,由此可得
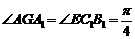 从而
从而 ,于是
,于是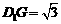
在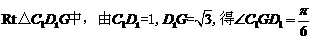
(Ⅱ)在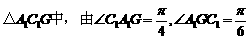 知
知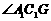 为钝角,
为钝角,
作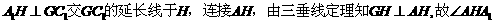
为二面角二面角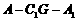 的平面角,
的平面角,
在 ,
,
从而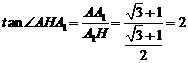 。
。
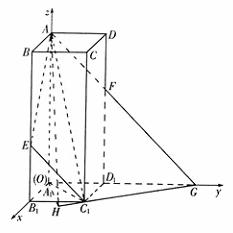 解法三:(Ⅰ)以
解法三:(Ⅰ)以 为原点,
为原点,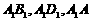 所在直线分别为x轴,y轴和z轴建立如图所示的空间直角坐标系。
所在直线分别为x轴,y轴和z轴建立如图所示的空间直角坐标系。
于是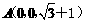 ,
,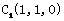 ,
, ,
, ,
,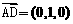 ,
,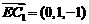
因为 和
和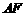 分别是平行平面
分别是平行平面 与平面
与平面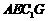 的交线,所以
的交线,所以 ,设
,设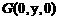 ,则
,则
由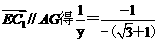 ,于是
,于是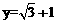
故 ,设异面直线AD与
,设异面直线AD与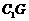 所成的角的大小为
所成的角的大小为 ,则
,则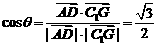 ,从而
,从而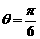 。
。
(Ⅱ)作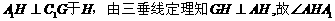 为二面角二面角
为二面角二面角
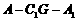 的平面角,设
的平面角,设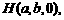 则
则
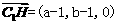 ,
,
由 得
得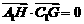 ,由此得
,由此得
又由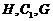 共线得
共线得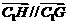 ,从而
,从而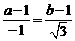 ,于是
,于是

联立(i)和(ii)得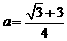 ,
, ,故
,故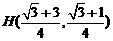
由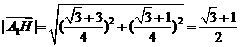 ,
,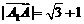
得: 。
。
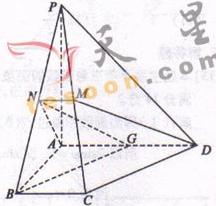
11.[06浙江·理]如图,在四棱锥 中,底面为直角梯形,
中,底面为直角梯形,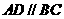 ,
,

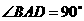 ,
, 底面
底面 ,且
,且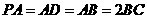 ,
,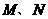 分别为
分别为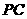 、
、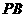 的中点。
的中点。
(Ⅰ)求证: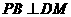 ;
;
(Ⅱ)求 与平面
与平面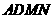 所成的角。
所成的角。
[解] 本题主要考查空间线线、线面关系、空间向量的概念与运算等基础知识,同时考查空间想象能力。
 方法一:
方法一:
(I)因为 是
是 的中点,
的中点,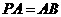 ,所以
,所以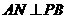 .
.
因为 平面
平面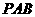 ,所以
,所以 ,
,
从而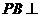 平面
平面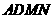 .因为
.因为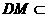 平面
平面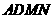 ,
,
所以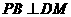 .
.
(II)取 的中点
的中点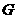 ,连结
,连结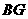 、
、 ,
,
则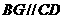 ,
,
所以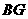 与平面
与平面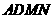 所成的角和
所成的角和 与平面
与平面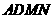 所成的角相等.
所成的角相等.
因为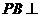 平面
平面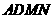 ,
,
所以 是
是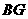 与平面
与平面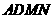 所成的角.
所成的角.
在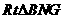 中,
中, 。
。
故 与平面
与平面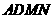 所成的角是
所成的角是 。
。
方法二:
如图,以 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系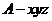 ,设
,设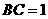 ,则
,则
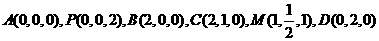 .
.
(I) 因为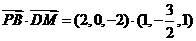
 ,所以
,所以
(II) 因为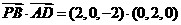
 ,所以
,所以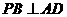 ,
,
又因为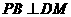 ,所以
,所以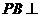 平面
平面
因此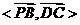 的余角即是
的余角即是 与平面
与平面 所成的角.
所成的角.
因为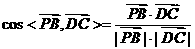
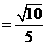 ,
,
所以 与平面
与平面 所成的角为
所成的角为 。
。
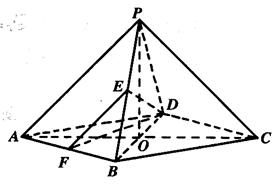
10.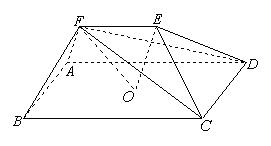 如图,在五面体
如图,在五面体 中,点
中,点 是矩形
是矩形 的对角线的交点,面
的对角线的交点,面 是等边三角形,棱
是等边三角形,棱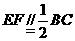 .
.
(1)证明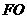 //平面
//平面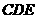 ;
;
(2)设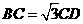 ,证明
,证明 平面
平面 .
.
[解] 本小题考查直线与平面平行、直线与平面垂直等基础知识,考查空间想象能力和推理论证能力.
(Ⅰ)证明:取CD中点M,连结OM.
在矩形ABCD中。  ,又
,又 ,
,
则 ,连结EM,于是四边形EFOM为平行四边形.
,连结EM,于是四边形EFOM为平行四边形. 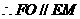
又 平面CDE,且EM
平面CDE,且EM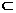 平面CDE,∵FO∥平面CDE
平面CDE,∵FO∥平面CDE
(Ⅱ)证明:连结FM,由(Ⅰ)和已知条件,在等边△CDE中,
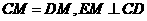 且
且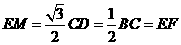 .
.
因此平行四边形EFOM为菱形,从而EO⊥FM
而FM∩CD=M, ∴CD⊥平面EOM,从而CD⊥EO.
而 ,
所以EO⊥平面CDF.
,
所以EO⊥平面CDF.
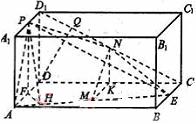
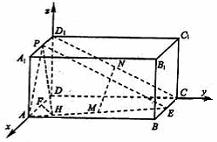
9.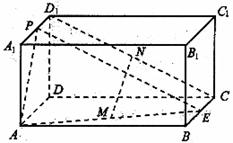 如图,长方体ABCD-
如图,长方体ABCD-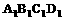 中,E、P分别是BC、
中,E、P分别是BC、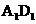 的中点,M、N分别是AE、
的中点,M、N分别是AE、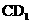 的中点,
的中点,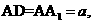
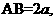
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求三棱锥P-DEN的体积。
[解] 本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。
解法一:(Ⅰ)证明:取 的中点
的中点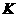 ,连结
,连结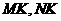
 ∵
∵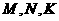 分别为
分别为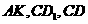 的中点
的中点
∵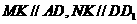
∴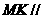 面
面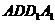 ,
, 面
面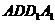
∴面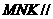 面
面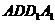 ∴
∴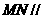 面
面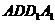
(Ⅱ)设 为
为 的中点
的中点
∵ 为
为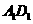 的中点
∴
的中点
∴ ∴
∴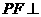 面
面
作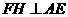 ,交
,交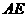 于
于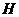 ,连结
,连结 ,则由三垂线定理得
,则由三垂线定理得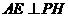
从而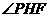 为二面角
为二面角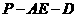 的平面角。
的平面角。
在 中,
中,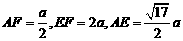 ,从而
,从而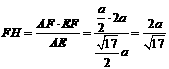
在 中,
中,
故:二面角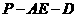 的大小为
的大小为 。
。
(Ⅲ)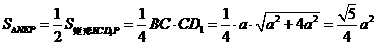
作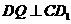 ,交
,交 于
于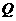 ,由
,由 面
面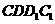 得
得
∴ 面
面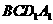
∴在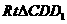 中,
中,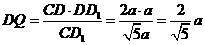
∴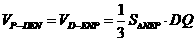
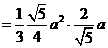
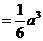 。
。
 方法二:以
方法二:以 为原点,
为原点, 所在直线分别为
所在直线分别为 轴,
轴, 轴,
轴,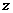 轴,建立直角坐标系,则
轴,建立直角坐标系,则
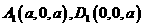
∵ 分别是
分别是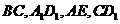 的中点
的中点
∴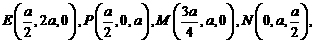
(Ⅰ) ,取
,取 ,显然
,显然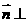 面
面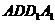
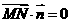 ,∴
,∴ 又
又 面
面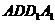 ∴
∴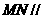 面
面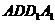
(Ⅱ)过 作
作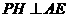 ,交
,交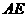 于
于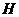 ,取
,取 的中点
的中点 ,则
,则
设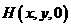 ,则
,则
又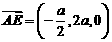
由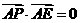 ,及
,及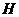 在直线
在直线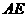 上,可得:
上,可得: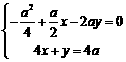
解得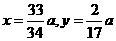
∴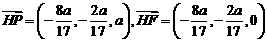 ∴
∴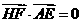 即
即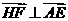
∴ 与
与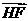 所夹的角等于二面角
所夹的角等于二面角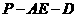 的大小
的大小
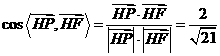
故:二面角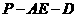 的大小为
的大小为 。
。
(Ⅲ)设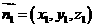 为平面
为平面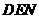 的法向量,则
的法向量,则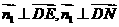
又
∴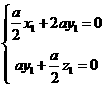 即
即 ∴可取
∴可取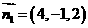
∴ 点到平面
点到平面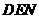 的距离为
的距离为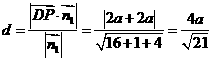 ,
,
∵ ,
,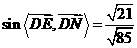 ,
,
∴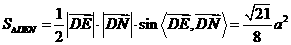 ,
,
∴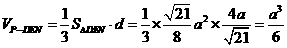 。
。
8.
在直三棱柱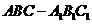 中,
中,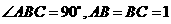 .
.
(1)求异面直线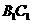 与
与 所成的角的大小;
所成的角的大小;
(2)若 与平面
与平面 所成角为
所成角为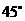 ,求三棱锥
,求三棱锥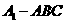 的体积。
的体积。
[解] (1) ∵BC∥B1C1, ∴∠ACB为异面直线B1C1与AC所成角(或它的补角)
∵∠ABC=90°,AB=BC=1, ∴∠ACB=45°,
∴异面直线B1C1与AC所成角为45°.
(2)∵AA1⊥平面ABC,
∠ACA1是A1C与平面ABC所成的角,∠ACA1=45°.
∵∠ABC=90°,AB=BC=1,AC=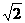 ∴AA1=
∴AA1=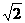 。
。
∴三棱锥A1-ABC的体积V=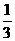 S△ABC×AA1=
S△ABC×AA1=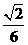 。
。
7. 在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60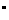 ,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60
,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60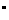 .
.
(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
[解](1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得
∠PBO是PB与平面ABCD所成的角,∠PBO=60°.
在Rt△AOB中BO=ABsin30°=1,由PO⊥BO,
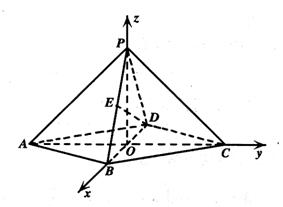 于是,PO=BOtg60°=
于是,PO=BOtg60°= ,
,
而底面菱形的面积为2 .
.
∴四棱锥P-ABCD的体积V=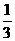 ×2
×2 ×
× =2.
=2.
(2)解法一:以O为坐标原点,射线OB、OC、OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.
在Rt△AOB中OA= ,于是,点A、B、D、P的坐标分别是A(0,-
,于是,点A、B、D、P的坐标分别是A(0,- ,0),B(1,0,0),D(-1,0,0),P(0,0,
,0),B(1,0,0),D(-1,0,0),P(0,0, )。
)。
E是PB的中点,则E(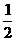 ,0,
,0,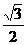 )。 于是
)。 于是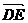 =(
=(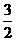 ,0,
,0,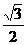 ),
), =(0,
=(0, ,
, ).
).
设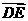 与
与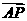 的夹角为θ,有cosθ=
的夹角为θ,有cosθ=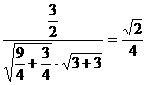 , θ=arccos
, θ=arccos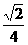 。
。
 ∴异面直线DE与PA所成角的大小是arccos
∴异面直线DE与PA所成角的大小是arccos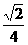 .
.
解法二:取AB的中点F,连接EF、DF.
由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成角(或它的补角)。
在Rt△AOB中AO=ABcos30°= =OP,
=OP,
于是,在等腰Rt△POA中,PA=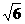 ,则EF=
,则EF=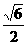 .
.
在正△ABD和正△PBD中,DE=DF= .
cos∠FED=
.
cos∠FED= =
=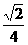
∴异面直线DE与PA所成角的大小是arccos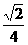 .
.
6.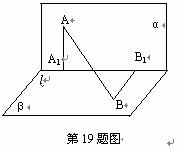 如图,α⊥β,α∩β=l , A∈α, B∈β,点A在直线l 上的射影为A1, 点B在l的射影为B1,已知AB=2,AA1=1, BB1=, 求:
如图,α⊥β,α∩β=l , A∈α, B∈β,点A在直线l 上的射影为A1, 点B在l的射影为B1,已知AB=2,AA1=1, BB1=, 求:
(I) 直线AB分别与平面α,β所成角的大小;
(II)二面角A1-AB-B1的大小。
[解] 解法一:(Ⅰ)如图, 连接A1B,AB1,
∵α⊥β, α∩β=l ,AA1⊥l, BB1⊥l,
∴AA1⊥β, BB1⊥α. 则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中, BB1= , AB=2,
∴sin∠BAB1 = = . ∴∠BAB1=45°.
Rt△AA1B中, AA1=1,AB=2, sin∠ABA1= = , ∴∠ABA1= 30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ)∵BB1⊥α, ∴平面ABB1⊥α。
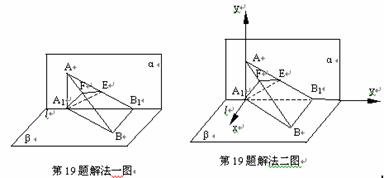 在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B。过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,
在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B。过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB,
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°, ∴AB1=B1B=.
∴Rt△AA1B中,
A1B== = 。
由AA1·A1B=A1F·AB得
A1F== = ,
∴在Rt△A1EF中,sin∠A1FE = = ,
∴二面角A1-AB-B1的大小为arcsin.
解法二:(Ⅰ)同解法一.
(Ⅱ)
如图,建立坐标系, 则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得=t , 即(x,y,z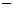 1)=t(,1,
1)=t(,1, 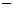 1), ∴点F的坐标为(t, t,1
1), ∴点F的坐标为(t, t,1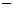 t).要使⊥,须·=0, 即(t, t,1
t).要使⊥,须·=0, 即(t, t,1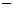 t) ·(,1,
t) ·(,1,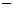 1)=0, 2t+t
1)=0, 2t+t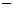 (1
(1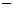 t)=0, 解得t= ,
t)=0, 解得t= ,
∴点F的坐标为(,, ), ∴=(,, ).
设E为AB1的中点,则点E的坐标为(0,, )。 ∴=(,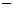 ,).
,).
又·=(,-,)·(,1, 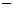 1)=
1)= 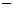
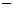 =0,
∴⊥,
=0,
∴⊥,
∴∠A1FE为所求二面角的平面角.
又cos∠A1FE= = = = = ,
∴二面角A1-AB-B1的大小为arccos.
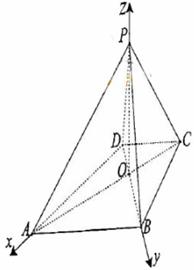
5. 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,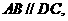

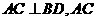 与
与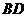 相交于点
相交于点 ,且顶点
,且顶点 在底面上的射影恰为
在底面上的射影恰为 点,又
点,又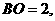
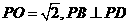 .
.
(Ⅰ)求异面直接 与
与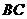 所成角的余弦值;
所成角的余弦值;
(Ⅱ)求二面角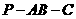 的大小;
的大小;
(Ⅲ)设点M在棱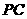 上,且
上,且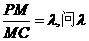 为何值时,
为何值时, 平面
平面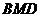 。
。
[解] 解法一: 平面
平面 ,
, 
又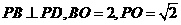 ,
,
由平面几何知识得: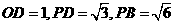
(Ⅰ)过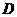 做
做 交于
交于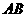 于
于 ,连结
,连结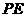 ,则
,则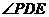 或其补角为异面直线
或其补角为异面直线 与
与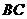 所成的角,
所成的角,

 四边形
四边形 是等腰梯形,
是等腰梯形,

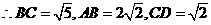
又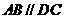
 四边形
四边形 是平行四边形。
是平行四边形。 
 是
是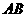 的中点,且
的中点,且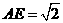
又 ,
, 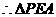 为直角三角形,
为直角三角形,
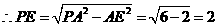
在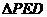 中,由余弦定理得:
中,由余弦定理得: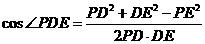
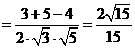
故异面直线PD与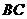 所成的角的余弦值为
所成的角的余弦值为 。
。
(Ⅱ)连结 ,由(Ⅰ)及三垂线定理知,
,由(Ⅰ)及三垂线定理知,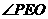 为二面角
为二面角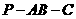 的平面角
的平面角
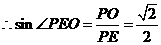 ,
, 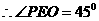
 二面角
二面角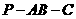 的大小为
的大小为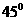
(Ⅲ)连结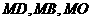 ,
,
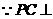 平面
平面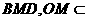 平面
平面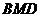 ,
,
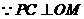
又在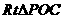 中,
中,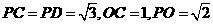 ,
,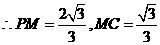 ,
,
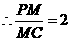 故
故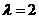 时,
时, 平面
平面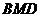
解法二:  平面
平面

又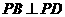 ,
,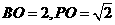 ,
,
由平面几何知识得:
以 为原点,
为原点,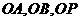 分别为
分别为 轴建立如图所示的空间直角坐标系,则各点坐标为
轴建立如图所示的空间直角坐标系,则各点坐标为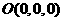 ,
, ,
, ,
,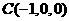 ,
,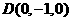 ,
,
(Ⅰ) ,
, 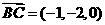 ,
,
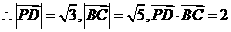 。
。 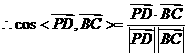
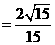 。
。
故直线 与
与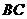 所成的角的余弦值为
所成的角的余弦值为 。
。
(Ⅱ)设平面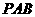 的一个法向量为
的一个法向量为 ,
,
由于 ,
,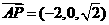 , 由
, 由 得
得 
取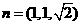 ,又已知平面ABCD的一个法向量
,又已知平面ABCD的一个法向量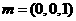 ,
,
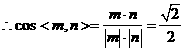 。
。
又二面角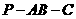 为锐角,
为锐角,
 所求二面角
所求二面角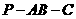 的大小为
的大小为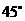
(Ⅲ)设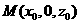 ,由于
,由于 三点共线,
三点共线, ,
,
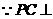 平面
平面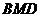

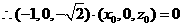
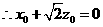
由(1)(2)知: ,
,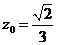 。
。 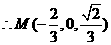
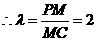
故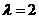 时,
时, 平面
平面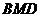 。
。
4.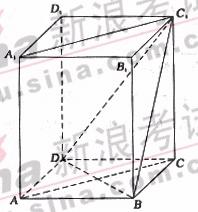 如图,
如图,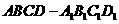 是正四棱柱。
是正四棱柱。
(I)求证:BD⊥平面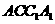 ;
;
(II)若二面角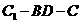 的大小为60°,求异面直线BC1与AC所成角的大小。
的大小为60°,求异面直线BC1与AC所成角的大小。
[解]解法一:(Ⅰ)∵ 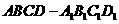 是正四棱柱,
是正四棱柱,
∴ CC1⊥平面ABCD, ∴ BD⊥CC1,
∵ ABCD是正方形, ∴ BD⊥AC
又 ∵AC,CC1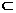 平面
平面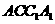 ,且AC∩CC1=C,
,且AC∩CC1=C,
 ∴ BD⊥平面
∴ BD⊥平面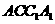
(II)设BD与AC相交于O,连接C1O。
∵ CC1⊥平面ABCD,BD⊥AC,
∴ BD⊥C1O,
∴ ∠C1OC是二面角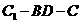 的平面角,
的平面角,
∴ ∠C1OC=60°。
连接A1B ∵ A1C1∥AC,
∴ ∠A1C1B是异面直线BC1与AC所成角。
设BC=a,则CO=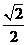 ,CC1=CO
,CC1=CO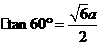 ,A1B=BC1=
,A1B=BC1= 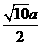 ,
,
 。
。
在△A1B1C1中,由余弦定理得 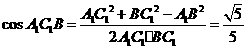 ,
,
∴ A1C1 B=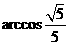 , ∴ 异面直线BC1与 AC所成的角的大小为
, ∴ 异面直线BC1与 AC所成的角的大小为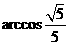 。
。
解法二:
 (I)建立空间直角坐标系D-xyz,如图。
(I)建立空间直角坐标系D-xyz,如图。
设AD=a,DD1=b,则有D(0,0,0),A(a,0,0,)、B(a,a,0,)、C(0,a,0,)、C1(0,a,b,)
∴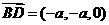 ,
,
 ,
,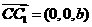
∴
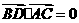 ,
,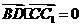
∴
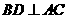 ,
, 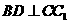 。
。
又∵AC,CC1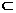 平面
平面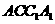 ,且AC∩CC1=C,
,且AC∩CC1=C,
∴ BD⊥平面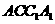
(Ⅱ)
设BD与AC相交于O,连接C1O,则点O坐标为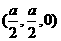 ,
,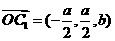
∵  ,
∴ BD⊥C1O ,又BD⊥CO
,
∴ BD⊥C1O ,又BD⊥CO
∴ ∠C1OC是二面角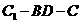 的平面角, ∴ ∠C1OC=60°。
的平面角, ∴ ∠C1OC=60°。
∴ 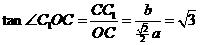 ,
∴
,
∴ 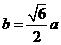 。
。
∵  ,
,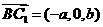 , ∴
, ∴ 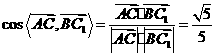
∴
异面直线BC1与 AC所成的角的大小为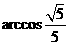 。
。
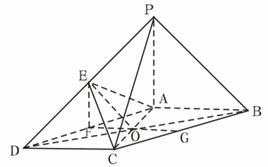
3.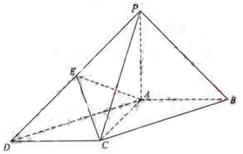 如图,在底面为平行四边形的四棱锥
如图,在底面为平行四边形的四棱锥 中,
中,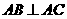 ,
, 平面
平面 ,且
,且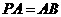 ,点
,点 是
是 的中点.
的中点.
(Ⅰ)求证: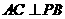 ;
;
(Ⅱ)求证: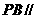 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
[解] 解法一:
(Ⅰ) PA
PA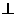 平面ABCD,
平面ABCD,
 AB是PB在平面ABCD上的射影,
AB是PB在平面ABCD上的射影,
又 AB
AB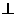 AC,AC
AC,AC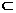 平面ABCD,
平面ABCD,
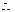 AC
AC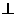 PB.
PB.
(Ⅱ)连接BD,与AC相交与O,连接EO,
 ABCD是平行四边形
ABCD是平行四边形 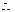 O是BD的中点
O是BD的中点
又E是PD的中点,
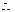 EO
EO PB.
PB.
又PB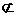 平面AEC,EO
平面AEC,EO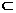 平面AEC,
平面AEC,
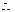 PB
PB 平面AEC,
平面AEC,
(Ⅲ)如图,取AD的中点F,连EF,FO,则
EF是△PAD的中位线,
\EF PA又
PA又 平面
平面 , \EF^平面
, \EF^平面
同理FO是△ADC的中位线,\FO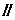 AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角. 又FO=
AB\FO^AC由三垂线定理可知\ÐEOF是二面角E-AC-D的平面角. 又FO=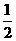 AB=
AB=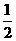 PA=EF。
PA=EF。
\ÐEOF=45°而二面角 与二面角E-AC-D互补,
与二面角E-AC-D互补,
故所求二面角 的大小为135°.
的大小为135°.
解法二:
(Ⅰ)建立空间直角坐标系A-xyz,如图。
设AC=a,PA=b。则有A(0,0,0)、B(0,b,0)、C(a,0,0)、P(0,0,b),
∴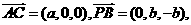 从而
从而
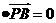 ,
,
∴
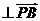 。
。
(Ⅱ)连结BD,与AC相交于O,连结EO。
由已知得 ,
,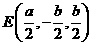 ,
,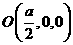 ,
,
 ∴
∴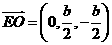 ,
,
又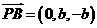 , ∴
, ∴ 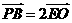 ,
,
∴ 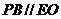 ,
,
又PB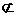 平面AEC,EO
平面AEC,EO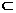 平面AEC。
平面AEC。
∴ PB 平面AEC。
平面AEC。
(Ⅲ)取BC中点G,连接OG,则点G的坐标为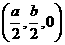 ,
,

又
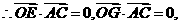
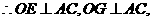
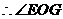 是二面角
是二面角 的平面角。
的平面角。


 二面角
二面角 的大小为
的大小为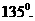
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com