
题目列表(包括答案和解析)
3.已知向量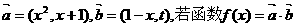 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
2.(Ⅰ)解: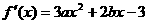 ,依题意,
,依题意,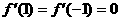 ,即
,即
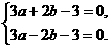 解得
解得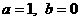 .
.
∴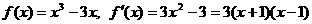 .
.
令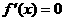 ,得
,得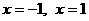 .
.
若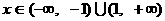 ,则
,则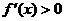 ,
,
故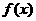 在
在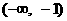 上是增函数,
上是增函数,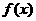 在
在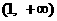 上是增函数.
上是增函数.
若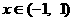 ,则
,则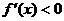 ,故
,故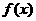 在
在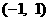 上是减函数.
上是减函数.
所以,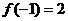 是极大值;
是极大值;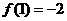 是极小值.
是极小值.
(Ⅱ)解:曲线方程为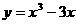 ,点
,点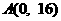 不在曲线上.
不在曲线上.
设切点为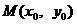 ,则点M的坐标满足
,则点M的坐标满足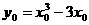 .
.
因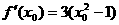 ,故切线的方程为
,故切线的方程为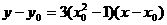
注意到点A(0,16)在切线上,有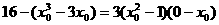
化简得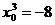 ,解得
,解得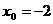 .
.
所以,切点为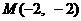 ,切线方程为
,切线方程为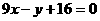 .
.
2.已知函数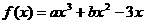 在
在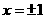 处取得极值.
处取得极值.
(Ⅰ)讨论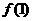 和
和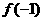 是函数
是函数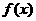 的极大值还是极小值;
的极大值还是极小值;
(Ⅱ)过点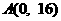 作曲线
作曲线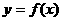 的切线,求此切线方程.
的切线,求此切线方程.
(Ⅰ)求函数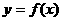 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数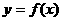 的单调区间.
的单调区间.
1.解:(Ⅰ)由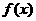 的图象经过P(0,2),知d=2,
的图象经过P(0,2),知d=2,
所以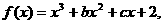
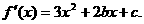
由在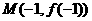 处的切线方程是
处的切线方程是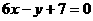 ,知
,知
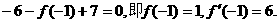
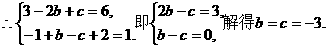
故所求的解析式是 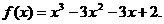
(Ⅱ)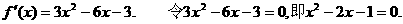
解得 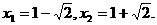 当
当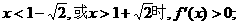
当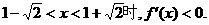
故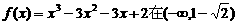 内是增函数,
内是增函数,
在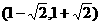 内是减函数,在
内是减函数,在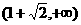 内是增函数.
内是增函数.
(2).设点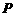 是曲线
是曲线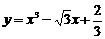 上的任意一点,
上的任意一点,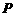 点处切线倾斜角为
点处切线倾斜角为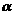 ,则角
,则角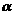 的取值范围是 。
的取值范围是 。
答案1、 2、
2、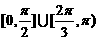
结合导数的判定单调性的方法,进行逆向分析求解。
A.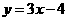 B。
B。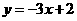 C。
C。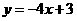 D。
D。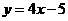
(2)
函数y=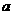 x2+1的图象与直线y=x相切,则
x2+1的图象与直线y=x相切,则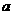 =
( )
=
( )
A. 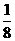 B.
B.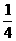 C.
C.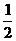 D.1
D.1
答案为:BB
运用导数几何意义进行分析求解。
以我们所学习的初等函数为背景,考察复合函数以及超越函数的最值问题,同时也考察对于参数的分类讨论,方向明确。估计09年的导数试题方向不变,但是在函数解析式方面要加以突破了,比如可能要考察与三角函数有关的函数的最值问题。
3.求函数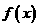 的单调区间:不等式
的单调区间:不等式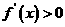 的解集为
的解集为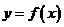 的增区间;不等式
的增区间;不等式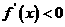 的解集为
的解集为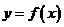 的减区间。(注:求函数的单调区间实质上是‘解不等式’)
的减区间。(注:求函数的单调区间实质上是‘解不等式’)
2. 设函数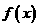 在
在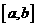 上连续,在
上连续,在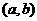 内可导,求
内可导,求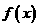 在
在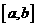 上的最值的步骤:
上的最值的步骤:
(1) 求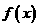 在
在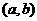 内的极值;(2)将
内的极值;(2)将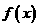 各极值与
各极值与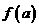 ,
,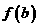 比较,确定
比较,确定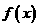 的最大和最小值。
的最大和最小值。
1. 求函数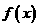 极值的步骤:
极值的步骤:
(1)
求导数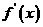 ;(2)求方程
;(2)求方程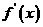 =0的根;(3)检查
=0的根;(3)检查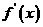 =0的根的左右区间对应的
=0的根的左右区间对应的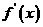 的符号:若左正右负,则
的符号:若左正右负,则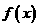 在这个根处取得极大值;若左负右正,则
在这个根处取得极大值;若左负右正,则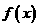 在这个根处取得极小值。(注:实质为‘解方程’,解关于
在这个根处取得极小值。(注:实质为‘解方程’,解关于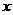 的方程
的方程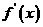 =0)
=0)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com