
题目列表(包括答案和解析)
18、.解:(1)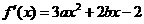 由条件知
由条件知
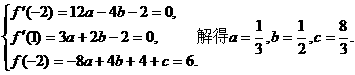
(2)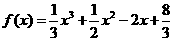 ,
,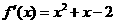
|
x |
-3 |
(-3,-2) |
-2 |
(-2,1) |
1 |
(1,3) |
3 |
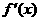 |
|
+ |
0 |
- |
0 |
+ |
|
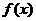 |
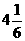 |
↗ |
6 |
↘ |
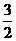 |
↗ |
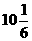 |
由上表知,在区间[-3,3]上,当x=3时,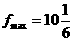 ,当x=1时,
,当x=1时,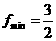 .
.
17、解:(Ⅰ)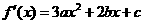 ,由已知
,由已知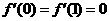 ,
,
即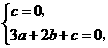 解得
解得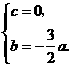
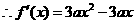 ,
,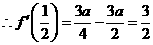 ,
,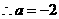 ,
,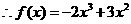 .
.
(Ⅱ)令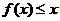 ,即
,即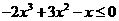 ,
,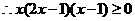 ,
,
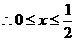 或
或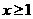 .又
.又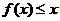 在区间
在区间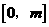 上恒成立,
上恒成立,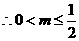 .
.
16、解:设楼房每平方米的平均综合费为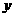 元,依题意得
元,依题意得
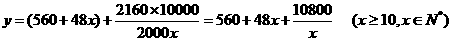
则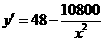 ,令
,令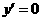 ,即
,即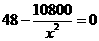 ,解得
,解得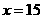
当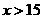 时,
时,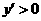 ;当
;当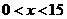 时,
时,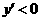 ,
,
因此,当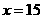 时,
时,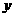 取得最小值,
取得最小值,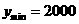 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层。
15、解:∵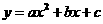 分别过(1,1)点和(2,-1)点
分别过(1,1)点和(2,-1)点
∴ a+b+c=1 (1) 4a+2b+c=-1 (2)
又 y′=2ax+b ∴y′|x=2=4a+b=1 (3)
由(1)(2)(3)可得,a=3,b=-11,c=9.
11、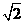 12、3 13、
12、3 13、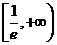 14、25
14、25
1、B 2、D 3、A 4、B 5、A 6、B 7、B 8、D 9、C 10、C
20、(本小题14分)
设函数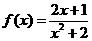 。
。
(Ⅰ)求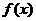 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若对一切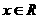 ,
,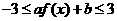 ,求
,求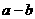 的最大值.
的最大值.
广州市育才中学2008-09学年高二数学选修1-1单元检测题
导数及其应用(A组:适合A,B类学校使用)key
19、(本小题14分)
已知二次函数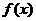 满足:(1)在
满足:(1)在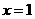 时有极值;(2)图象过点
时有极值;(2)图象过点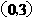 ,且在该点处的切线与直线
,且在该点处的切线与直线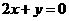 平行.
平行.
(I)求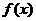 的解析式;
的解析式;
(II)求函数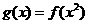 的单调递增区间.
的单调递增区间.
18、(本小题14分)
已知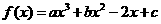 在
在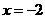 时有极大值6,在
时有极大值6,在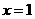 时有极小值,求a,b,c的值;并求
时有极小值,求a,b,c的值;并求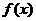 区间
区间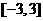 上的最大值和最小值.
上的最大值和最小值.
17、(本小题14分)
已知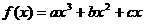 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间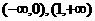 上是减函数,又
上是减函数,又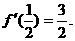 .
.
(Ⅰ)求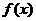 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有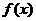 ≤x成立,求m的取值范围。
≤x成立,求m的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com