
题目列表(包括答案和解析)
1.点P与定点F(2,0)的距离与它到定直线x=8的距离之比为1:2,求点P的轨迹方程.
2. 椭圆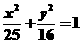 上的点M到左准线的距离是5,求M到右焦点的距离.
上的点M到左准线的距离是5,求M到右焦点的距离.

 例2.
例2.
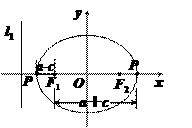
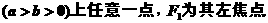 求|PF1|的最小值和最大值.
求|PF1|的最小值和最大值.
练习2
1.求下列椭圆焦点坐标和准线方程:

1.椭圆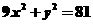 的长轴长为 18 ,短轴长为 6 ,半焦距为
的长轴长为 18 ,短轴长为 6 ,半焦距为 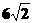 ,离心率为
,离心率为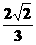 ,焦点坐标为
,焦点坐标为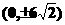 ,顶点坐标为
,顶点坐标为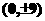 ,
,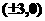 .
.
[讲授新课]
例1 如图,设M(x,y)与定点F(4,0)的距离和它到直线l: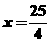 的距离的比是常数
的距离的比是常数 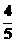 ,
,
求点M的轨迹方程.
练习1
2.1.2椭圆的简单几何性质(二)
教学目标: 椭圆的范围、对称性、对称中心、离心率及顶点(截距).
重点难点分析
教学重点:椭圆的简单几何性质.
教学难点:椭圆的简单几何性质.
教学设计:
[复习引入]
4. 如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示
椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①
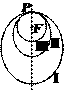 a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c2;④
a1+c1=a2+c2;②a1-c1=a2-c2;③c1a2>a1c2;④ 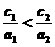 .
.
其中正确式子的序号是( B )
A.①③ B.②③ C. ①④ D.②④
本资料由《七彩教育网》 提供!
3. F1、F2 为椭圆的两个焦点,过F2的直线交椭圆于P、Q两点,PF1⊥PQ,且|PF1|=|PQ|,求椭圆的离心率.
3. 当m取何值直线l : y=x+m与椭圆9x2+16y2=144相切、相交、相离.
讲授新课
例1已知椭圆的两个焦点为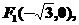
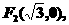 离心率为
离心率为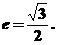
(1)求椭圆的方程;
(2)设直线l:y=x+m,若l与椭圆交于P、Q两点,且∣PQ∣等于椭圆的短轴长,求m的值.
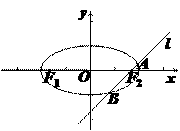
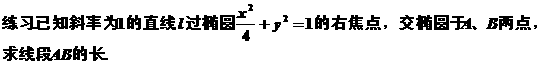
例2 已知椭圆的中心在原点,焦点在x轴上,直线y=x+1与该椭圆交于点P、Q,且
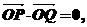
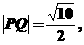 求椭圆的方程.
求椭圆的方程.
例3 已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4.
(1)求椭圆的方程;
(2)直线l过点P(0,2)且与椭圆相交于A、B两点,当△AOB面积取得最大值时,求直线l的方程.
课后作业
《学案》P38面双基训练.
本资料由《七彩教育网》 提供!
2.1.2 椭圆的简单几何性质(四)
复习导入


18.(满分12分)设数列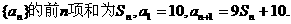
(1)求证: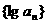 是等差数列;
是等差数列;
 (2)设
(2)设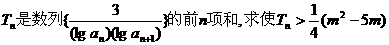 对所有的
对所有的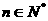 都成立的最大正整数m的值.
都成立的最大正整数m的值.
[附加题](满分10分,记入总分)已知数列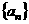 的前
的前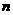 项和
项和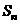 满足
满足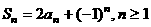 .
.
(1)写出数列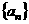 的前三项
的前三项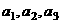 ;(2)求数列
;(2)求数列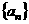 的通项公式;
的通项公式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com