
题目列表(包括答案和解析)
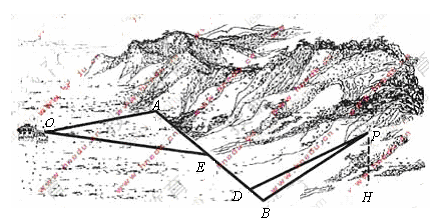
28.如图4,某地为了开发旅游资源,欲修建一条连接风景点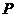 和居民区
和居民区 的公路,点
的公路,点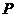 所在的山坡面与山脚所在水平面
所在的山坡面与山脚所在水平面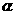 所成的二面角为
所成的二面角为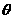 (
(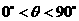 ),且
),且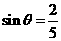 ,点
,点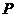 到平面
到平面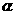 的距离
的距离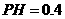 (km).沿山脚原有一段笔直的公路
(km).沿山脚原有一段笔直的公路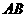 可供利用.从点
可供利用.从点 到山脚修路的造价为
到山脚修路的造价为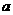 万元/km,原有公路改建费用为
万元/km,原有公路改建费用为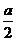 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为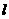 km(
km(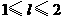 )时,其造价为
)时,其造价为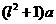 万元.已知
万元.已知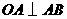 ,
,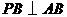 ,
,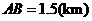 ,
,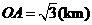 .
.
(I)在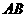 上求一点
上求一点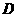 ,使沿折线
,使沿折线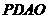 修建公路的总造价最小;
修建公路的总造价最小;
(II) 对于(I)中得到的点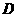 ,在
,在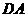 上求一点
上求一点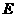 ,使沿折线
,使沿折线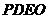 修建公路的总造价最小.
修建公路的总造价最小.
(III)在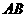 上是否存在两个不同的点
上是否存在两个不同的点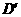 ,
,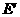 ,使沿折线
,使沿折线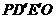 修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(II)中得到的最小总造价,证明你的结论.

答案解析
27.设二次函数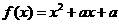 ,方程
,方程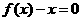 的两根
的两根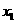 和
和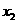 满足
满足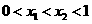 .
.
(I)求实数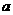 的取值范围;
的取值范围;
(II)试比较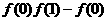 与
与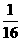 的大小.并说明理由.
的大小.并说明理由.
26.已知定义在正实数集上的函数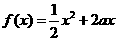 ,
,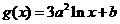 ,其中
,其中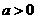 .设两曲线
.设两曲线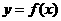 ,
,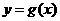 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用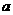 表示
表示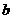 ,并求
,并求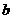 的最大值;
的最大值;
(II)求证: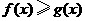 (
(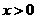 ).
).
25.设函数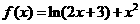
(Ⅰ)讨论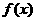 的单调性;
的单调性;
(Ⅱ)求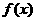 在区间
在区间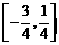 的最大值和最小值.
的最大值和最小值.
24.设函数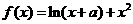
(I)若当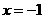 时,
时,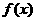 取得极值,求
取得极值,求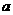 的值,并讨论
的值,并讨论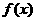 的单调性;
的单调性;
(II)若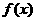 存在极值,求
存在极值,求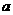 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于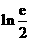 .
.
23.已知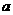 是实数,函数
是实数,函数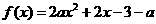 .如果函数
.如果函数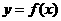 在区间
在区间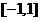 上有
上有
零点,求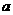 的取值范围.
的取值范围.
22、解:由已知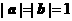 . ∵
. ∵ 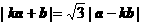 ,
,
∴ 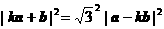 .
.
∴ 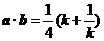 . ∵ k>0, ∴
. ∵ k>0, ∴ 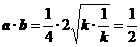 .
.
此时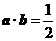 ∴
∴ 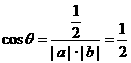 . ∴
. ∴ 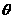 =60°.
=60°.
21、解析:设f(x)的二次项系数为m,其图象上两点为(1-x,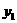 )、B(1+x,
)、B(1+x,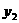 )因为
)因为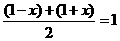 ,
,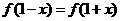 ,所以
,所以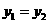 ,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
,由x的任意性得f(x)的图象关于直线x=1对称,若m>0,则x≥1时,f(x)是增函数,若m<0,则x≥1时,f(x)是减函数.
∵ 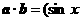 ,
,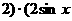 ,
,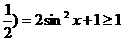 ,
,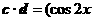 ,
,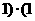 ,
,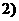
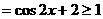 ,
,
∴ 当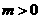 时,
时,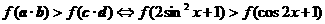
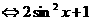
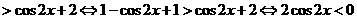
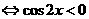
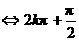
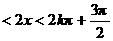 ,
,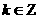 .
.
∵ 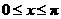 , ∴
, ∴ 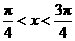 .
.
当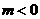 时,同理可得
时,同理可得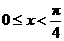 或
或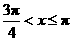 .
.
综上: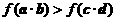 的解集是当
的解集是当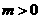 时,为
时,为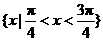 ;
;
当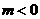 时,为
时,为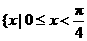 ,或
,或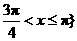 .
.
20、解析:∵ 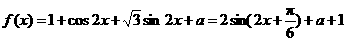
(1)最小正周期 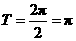
(2)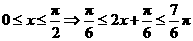 ,
,
∴ 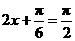 时
时 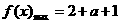 ,∴
,∴ 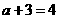 , ∴ a=1.
, ∴ a=1.
19、
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com