
题目列表(包括答案和解析)
6、解:(1)当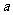 =0时,函数
=0时,函数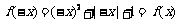 ,此时
,此时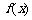 为偶函数.
为偶函数.
当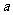 ≠0时,
≠0时,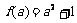 ,
,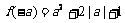 ,
,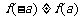 .
.
此时函数f(x)为非奇非偶函数.
(2)当x≥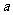 时,函数
时,函数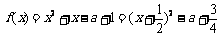 .
.
若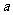 ≤-
≤-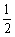 ,则函数
,则函数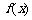 在
在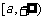 上的最小值为
上的最小值为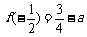 .
.
若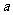 >-
>-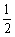 ,则函数
,则函数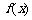 在
在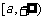 上单调递增,从而,函数
上单调递增,从而,函数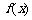 在
在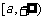 上的最小值为f(
上的最小值为f(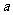 )=
)=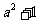 .
.
综上,当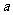 ≤-
≤-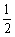 时,函数f(x)的最小值是
时,函数f(x)的最小值是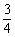 -
-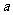 .
.
当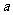 >-
>-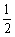 时,函数f(x)的最小值是
时,函数f(x)的最小值是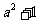 .
.
5、解:(1)∵f(x)=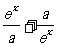 是R上的偶函数,∴f(x)-f(-x)=0.
是R上的偶函数,∴f(x)-f(-x)=0.
∴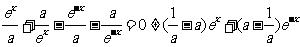
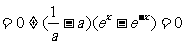
ex-e-x不可能恒为“0”, ∴当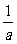 -a=0时等式恒成立,∴a=1.
-a=0时等式恒成立,∴a=1.
(2)在(0,+∞)上任取x1<x2,
f(x1)-f(x2)=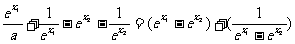
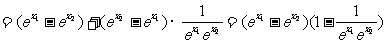
∵e>1,∴0<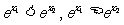 >1,∴
>1,∴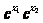 >1
>1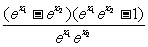 <0,
<0,
∴f(x1)-f(x2)<0,
∴f(x)是在(0,+∞)上的增函数.
4、解: (1)法一: 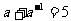 ,两边平方得:
,两边平方得: 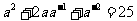 ,即
,即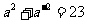
法二(配方): 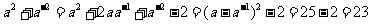
(2)∵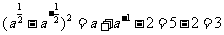 , ∴
, ∴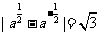 , ∴
, ∴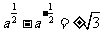
(3)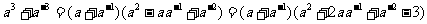
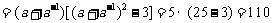
3、解:因为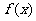 是奇函数,所以
是奇函数,所以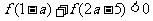 可变为
可变为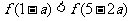
所以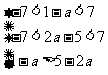 ,解得:
,解得: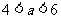
所以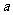 的取值范围为
的取值范围为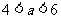 .
.
2、解:由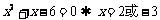 ,因此,
,因此,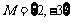 .
.
(i)若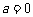 时,得
时,得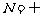 ,此时,
,此时,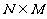 ;
;
(ii)若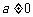 时,得
时,得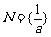 . 若
. 若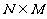 ,满足
,满足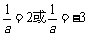 ,解得
,解得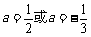 .
.
故所求实数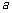 的值为
的值为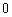 或
或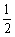 或
或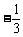 .
.
1、解:(1) 由于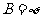 ,则有
,则有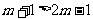 ,得
,得 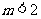 ,
,
故所求实数m的取值范围为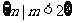 .
.
(2) 当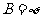 时,即
时,即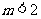 时,符合题意;
时,符合题意;
当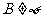 时,则只需
时,则只需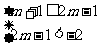 或
或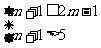 ,即
,即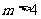 ,
,
故所求实数m的取值范围是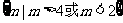 .
.
12. (本题12分)已知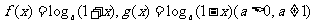 .
.
(1)求函数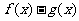 的定义域;
的定义域;
(2)判断函数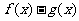 的奇偶性,并予以证明;
的奇偶性,并予以证明; 

(3)求使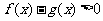 的
的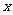 的取值范围.
的取值范围.
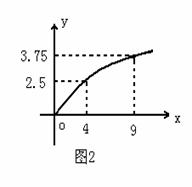
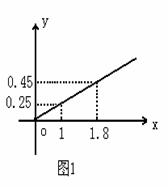
11.(本题12分)某民营企业生产A,B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润与投资单位是万元)
(1)分别将A,B两种产品的利润表示为投资的函数,并写出它们的函数关系式. 

(2)该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能是企业获得最大利润,其最大利润约为多少万元(精确到1万元).
10. (本题12分)已知奇函数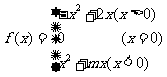 .
. 

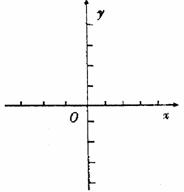
(1)求实数m的值,并在给出的直角坐标系中画出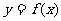 的图象;
的图象;
(2)若函数f(x)在区间[-1,|a|-2]上单调递增,试确定a的取值范围.
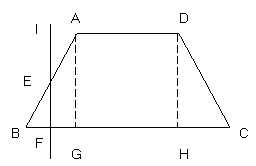
9. (本题12分)如图,已知底角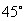 的等腰梯形ABCD,底边BC长为7cm,腰长为
的等腰梯形ABCD,底边BC长为7cm,腰长为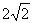 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=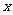 ,试写出左边部分的面积
,试写出左边部分的面积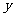 与
与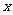 的函数解析式,并画出大致图象.
的函数解析式,并画出大致图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com