
题目列表(包括答案和解析)
20.解:(1)当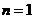 时,
时,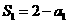 ,则
,则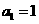
当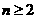 时 ,
时 ,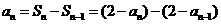
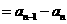 ,则
,则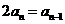
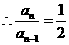
所以,数列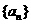 是以首项
是以首项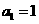 ,公比为
,公比为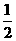 的等比数列,从而
的等比数列,从而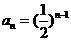
(2)
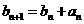
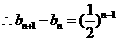
当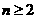 时,
时,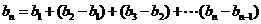
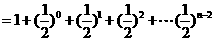
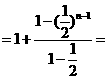
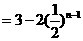
又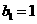 满足,
满足,
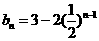
(3)
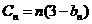
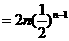
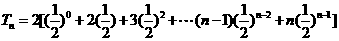 ①
①
而 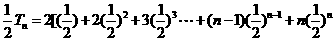 ②
②
①-②得: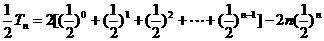
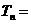
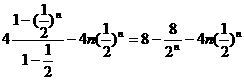
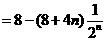
19.解:由题意得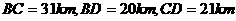

在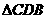 中由余弦定理得
中由余弦定理得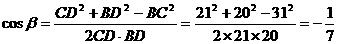
于是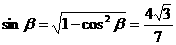 ,则
,则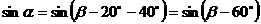
=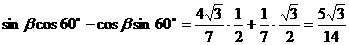 。
。
在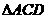 中,由正弦定理得
中,由正弦定理得
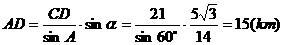
答:此人还得走15km到达A城
17.解:由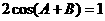 得
得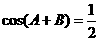 ,即
,即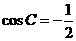 ,则
,则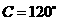

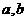 是方程
是方程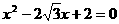 的两个根,
的两个根,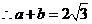 ,
,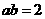
(1)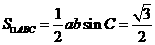
(2)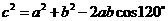
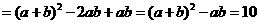 ,则
,则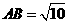
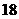 解:
解: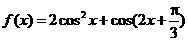
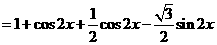
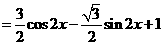
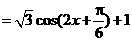
(1)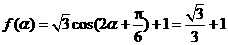 ,则
,则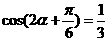
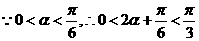 ,
,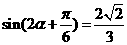
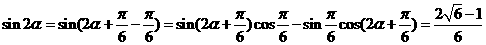 (2)
(2)
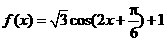 .
.
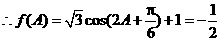 ,所以
,所以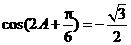 .
.
又因为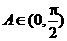 ,所以
,所以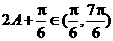 ,所以
,所以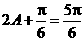 ,即
,即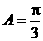 .
.
又因为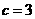 ,
,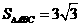 且
且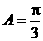 ,所以
,所以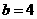 .
.
由余弦定理得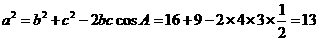 .
.
解得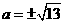 (舍负),所以
(舍负),所以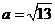 .
.
11.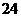 12.
12.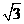 13.
13.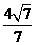 14.
14.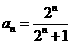 15.①②④
15.①②④
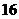 .解:设这三个数为
.解:设这三个数为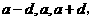 则
则
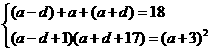 ,解得
,解得
所以这个数列为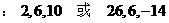
20.(本小题满分13分)对于数列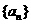 ,规定数列
,规定数列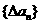 为数列
为数列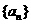 的一阶差分数列,其中
的一阶差分数列,其中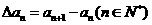 ;一般地,规定
;一般地,规定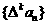 为
为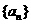 的
的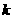 阶差分数列,其中
阶差分数列,其中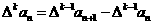 ,且
,且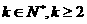 .
.
(1)已知数列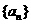 的通项公式
的通项公式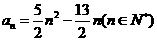 ,试证明
,试证明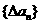 是等差数列;
是等差数列;
(2)若数列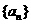 的首项
的首项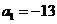 ,且满足
,且满足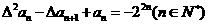 ,求数列
,求数列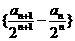 及
及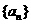 的通项公式;
的通项公式;
(3)在(2)的条件下,判断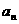 是否存在最小值,若存在求出其最小值,若不存在说明理由.
是否存在最小值,若存在求出其最小值,若不存在说明理由.
w.w.^w.k.&s.5*u.c.21.(本题满分14分)已知数列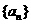 、
、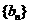 满足:
满足: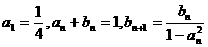 .
.
(1)求证:数列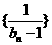 是等差数列;
是等差数列;
(2)求数列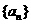 的通项公式;
的通项公式;
(3)设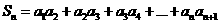 ,若
,若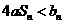 对于
对于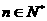 恒成立,试求实数
恒成立,试求实数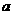 的取值范围.
的取值范围.
理科答案
1-5 6-10
6-10
20.(本题满分13分)设数列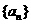 的前
的前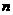 项和为
项和为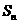 ,且满足
,且满足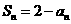 (
(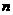 =1,2,3,…).
=1,2,3,…).
(1)求数列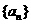 的通项公式;
的通项公式;
(2)若数列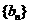 满足
满足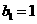 ,且
,且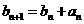 ,求数列
,求数列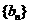 的通项公式;
的通项公式;
(3)设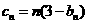 ,求数列
,求数列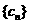 的前
的前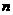 项和
项和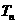 .
.
(8,9,10班学生做下面的题)
19.(本题满分12分)已知函数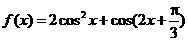
(1)若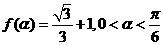 ,求
,求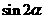 的值;
的值;
(2)在锐角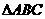 中,
中,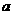 ,
,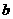 ,
,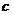 分别是角
分别是角 ,
,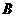 ,
,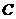 的对边;若
的对边;若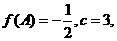
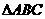 的面积
的面积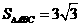 ,求
,求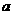 的值.
的值.
18.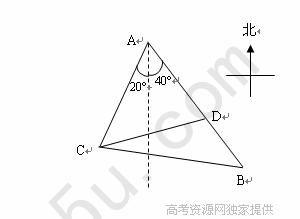 (本题满分12分) 如图,某观测站
(本题满分12分) 如图,某观测站 在城
在城 的南偏西
的南偏西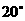 的方向上,由
的方向上,由 城出发有一公路,走向是南偏东
城出发有一公路,走向是南偏东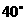 ,在
,在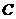 处测得距
处测得距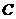 为31公里的公路上
为31公里的公路上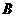 处,有一人正沿公路向
处,有一人正沿公路向 城走去,走了20公里后,到达
城走去,走了20公里后,到达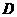 处,此时
处,此时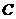 、
、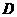 间距离为
间距离为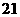 公里,问此人还需要走多少公里到达
公里,问此人还需要走多少公里到达 城.
城.
17.(本题满分12分)在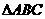 中,
中, 是方程
是方程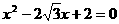 的两个根,且
的两个根,且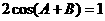
(1)求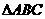 的面积;
的面积;
(2)求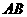 的长度.
的长度.
16.(本题满分12分)成等差数列的三个数的和等于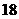 ,并且这三个数分别加上
,并且这三个数分别加上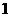 ,
,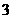 ,
,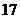 后就成了等比数列,求这三个数排成的等差数列.
后就成了等比数列,求这三个数排成的等差数列.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com