1．已知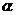是锐角，那么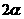是　　 (　 　)

A．第一象限角　　　 　　　 B．第二象限角　 　

　　C．小于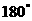的正角　　　 　　D．不大于直角的正角

17．(8分)已知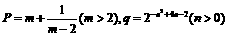：，试比较p与q的大小．

(1)求数列{a_n}的通项公式；

(2)令b_n = a_n·3ⁿ，求数列{b_n}的前n项之和为S_n．

19(10分)．若关于x的不等式mx² – (2m + 1)x + m – 10的解集为R，求m的取值范围．

20(10分)．某林场原有森林木材存储量为33万立方米，森林木材每年以25%的生长率增长，而每年冬天要砍伐的森林木材量为x。为了

[独家]实现经过20年达到森林木材存量翻两翻的目标，那么每年冬天的砍伐森林量不能超过多少？(假设lg₂ = 0.3)

21(10分)．已知：在数列{a_n}中，a₁ = 0，a_{n + 1}a_n – 2a_{n + 1} + 1 = 0，S_n是数列{a_n}前n项之和．

　　 (1)求证：数列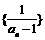为等差数列；

　　 (2)已知：当x＞0时，ln (1 + x)＜x恒成立，求证：S_n＜n – ln (1 + n)；

　　 (3)设b_n = 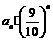，求证：对任意的正整数n，m均有|b_n – b_m|＜．

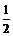2009-2010学年度第二学期期中考试

15．　　　　　 　　　

12． 　　　　　　　　　　　　　　　　　　　　　　　 13．　　　　 　　　　　　 14．　　 　　　　　

9．　　　　　　　 　　　　　　　　　　　　　　　 10．　 　　　　　　　　　　 11．　 　　　　　　　

18．(9分)已知：在等差数列{a_n}中，a₁ = 2，a₁ + a₂ + a₃ = 12．

(1)求数列{a_n}的通项公式；

(2)令b_n = a_n·3ⁿ，求数列{b_n}的前n项之和为S_n．

19(10分)．若关于x的不等式mx² – (2m + 1)x + m – 10的解集为R，求m的取值范围．

20(10分)．某林场原有森林木材存储量为33万立方米，森林木材每年以25%的生长率增长，而每年冬天要砍伐的森林木材量为x。为了实现经过20年达到森林木材存量翻两翻的目标，那么每年冬天的砍伐森林量不能超过多少？(假设lg₂ = 0.3)

21(10分)．已知：在数列{a_n}中，a₁ = 0，a_{n + 1}a_n – 2a_{n + 1} + 1 = 0，S_n是数列{a_n}前n项之和．

　　 (1)求证：数列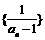为等差数列；

　　 (2)已知：当x＞0时，ln (1 + x)＜x恒成立，求证：S_n＜n – ln (1 + n)；

　　 (3)设b_n = 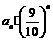，求证：对任意的

[独家]正整数n，m均有|b_n – b_m|＜．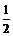

长沙市一中2009-2010学年度第二期期中考试

高一·数学

满分：100分　　 时量：115分钟

17．(8分)已知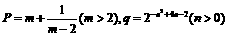：，试比较p与q的大小．

16．(8分)已知：某简单组合体的三视图及相关数据如右图所示．

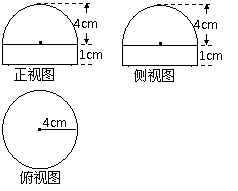(1)说出该简单组合体的构成；

(2)计算该简单组合体的体积．

15．设数列{a_n}的前n项之和为S_n，令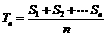，称T_n为数列a₁，a₂，…a_n的理想数，如果a₁，a₂，…a₅₀₀的理想数为2004，那么数列7，a₁，a₂，…a₅₀₀的理想数为　　 ．

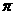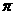14．圆台的上，下底面面积分别为，4 侧面面积为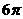。则圆台的母线长为　　　　 ．