
题目列表(包括答案和解析)
4、用反证法证明命题“三角形的内角中至少有一个不大于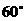 ”时,反设正确的是( )
”时,反设正确的是( )
A. 假设三内角都不大于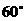 B. 假设三内角都大于
B. 假设三内角都大于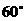
C. 假设三内角至多有一个大于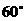 D. 假设三内角至多有两个大于
D. 假设三内角至多有两个大于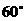
3、设数列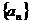 满足
满足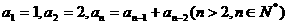 ,又通过公式
,又通过公式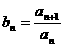 构造一个新的数列
构造一个新的数列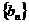 , 则
, 则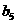 =( )
=( )
A. 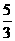 B.
B.
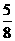 C.
C. 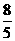 D.
D. 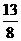
2、下列四个命题中,正确的有( )个。
①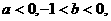 则
则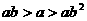 ②
②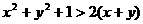
③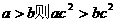 ④当
④当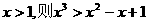
A. 1 B. 2 C. 3 D. 4
1、设全集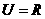 ,且
,且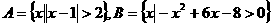 ,则
,则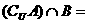 ( )
( )
A. 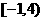 B.
B.
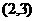 C.
C. 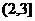 D.
D. 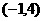
21.解:(1)当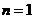 时,
时,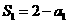 ,则
,则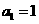
当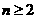 时 ,
时 ,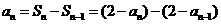
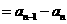 ,则
,则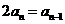
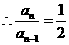
所以,数列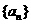 是以首项
是以首项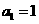 ,公比为
,公比为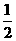 的等比数列,从而
的等比数列,从而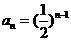
(2)
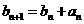
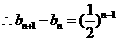
当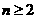 时,
时,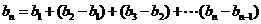
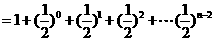
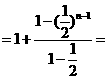
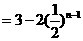 又
又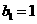 满足,
满足,
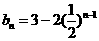
(3)
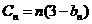
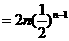
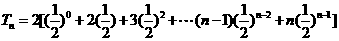 ①
①
而 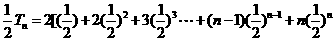 ②
②
①-②得: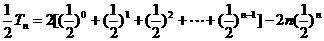
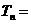
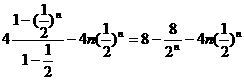
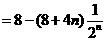
19.解:由题意得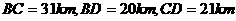

在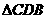 中由余弦定理得
中由余弦定理得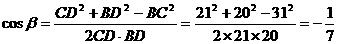
于是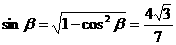 ,则
,则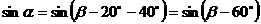
=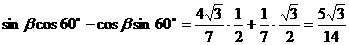 。
。
在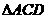 中,由正弦定理得
中,由正弦定理得
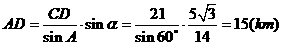
答:此人还得走15km到达A城
20解: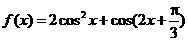
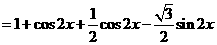
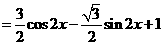
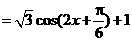
(1)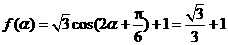 ,则
,则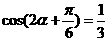
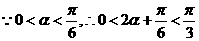 ,
,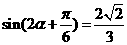
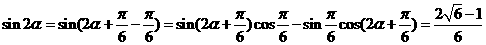 (2)
(2)
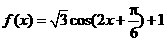 .
.
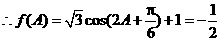 ,所以
,所以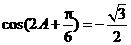 .
.
又因为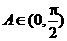 ,所以
,所以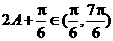 ,所以
,所以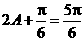 ,即
,即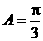 .
.
又因为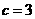 ,
,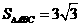 且
且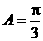 ,所以
,所以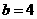 .
.
由余弦定理得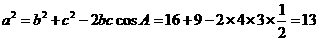 .
.
解得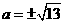 (舍负),所以
(舍负),所以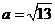 .
.
18.解:(1)设等差数列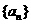 首项为
首项为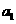 ,公差为
,公差为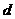 ,由题意,得
,由题意,得
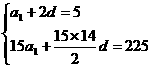 解得
解得 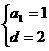
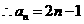
(2)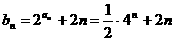 ,
,
∴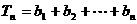
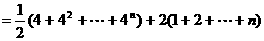
=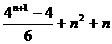
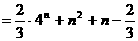
17.解:由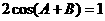 得
得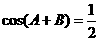 ,即
,即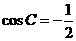 ,则
,则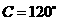

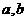 是方程
是方程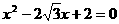 的两个根,
的两个根,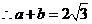 ,
,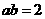
(1)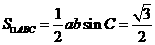
(2)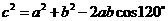
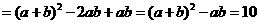 ,则
,则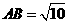
11.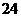 12.
12.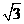 13.
13.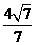 14.
14.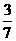 15.①②④
15.①②④
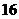 .解:设这三个数为
.解:设这三个数为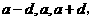 则
则
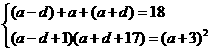 ,解得
,解得
所以这三个数为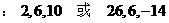
21.(本题满分14分)设数列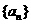 的前
的前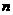 项和为
项和为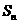 ,且满足
,且满足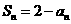 (
(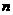 =1,2,3,…).
=1,2,3,…).
(1)求数列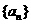 的通项公式;
的通项公式;
(2)若数列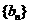 满足
满足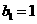 ,且
,且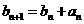 ,求数列
,求数列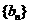 的通项公式;
的通项公式;
(3)设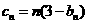 ,求数列
,求数列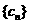 的前
的前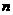 项和
项和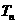 .
.
文科答案
1-5 6-10
6-10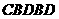
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com