
题目列表(包括答案和解析)
1 用“二分法”求方程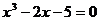 在区间
在区间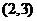 内的实根,取区间中点为
内的实根,取区间中点为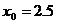 ,那么下一个有根的区间是
,那么下一个有根的区间是
2 函数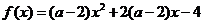 的定义域为
的定义域为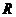 ,值域为
,值域为 ,则满足条件的实数
,则满足条件的实数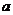 组成的集合是
组成的集合是
3 当 时,函数
时,函数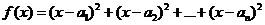 取得最小值
取得最小值
15 已知函数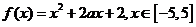
① 当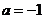 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;
② 求实数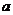 的取值范围,使
的取值范围,使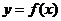 在区间
在区间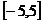 上是单调函数
上是单调函数
16 已知集合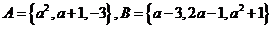 ,若
,若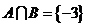 ,
,
求实数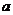 的值
的值
17 某商品进货单价为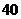 元,若销售价为
元,若销售价为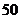 元,可卖出
元,可卖出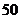 个,如果销售单价每涨
个,如果销售单价每涨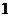 元,
元,
销售量就减少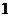 个,为了获得最大利润,则此商品的最佳售价应为多少?
个,为了获得最大利润,则此商品的最佳售价应为多少?
B卷 (总分50分)
14.若二次函数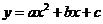 的图象与x轴交于
的图象与x轴交于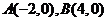 ,且函数的最大值为
,且函数的最大值为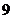 ,
,
则这个二次函数的表达式是
13. 已知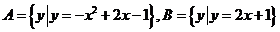 ,则
,则 _________
_________
11.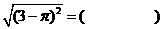 12.
12.
1 若集合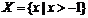 ,下列关系式中成立的为( )
,下列关系式中成立的为( )
A 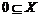 B
B 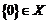 C
C 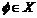 D
D 
2 下列四个集合中,是空集的是 ( )
A 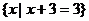 B
B 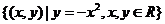
C 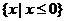 D
D 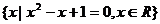
3.下列函数中,在区间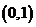 上是增函数的是 ( )
上是增函数的是 ( )
A 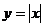 B
B 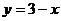
C 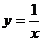 D
D 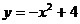
4 下列四个函数中是幂函数的是( )
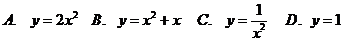
5 已知函数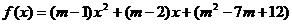 为偶函数,
为偶函数,
则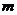 的值是
( )
的值是
( )
A 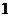 B
B 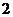
C 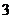 D
D 
6 若集合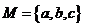 中的元素是△
中的元素是△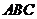 的三边长,则△
的三边长,则△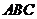 一定不是( )
一定不是( )
A 锐角三角形 B 直角三角形
C 钝角三角形 D 等腰三角形
7 若全集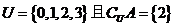 ,则集合
,则集合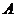 的真子集共有 ( )
的真子集共有 ( )
A 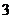 个 B
个 B 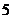 个 C
个 C 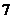 个 D
个 D  个
个
8 已知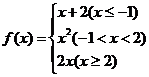 ,若
,若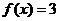 ,则
,则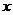 的值是( )
的值是( )
A 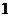 B
B 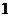 或
或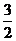 C
C 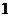 ,
,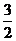 或
或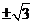 D
D 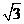
9 如果二次函数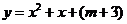 有两个不同的零点,则
有两个不同的零点,则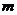 的取值范围是( )
的取值范围是( )
A 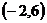 B
B 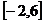 C
C 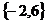 D
D 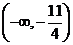
10 如果奇函数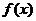 在区间
在区间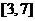 上是增函数且最大值为
上是增函数且最大值为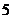 ,
,
那么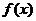 在区间
在区间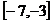 上是( )
上是( )
A 增函数且最小值是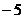 B 增函数且最大值是
B 增函数且最大值是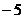
C 减函数且最大值是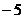 D 减函数且最小值是
D 减函数且最小值是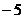
17(本小题10分)已知集合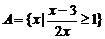 ,集合
,集合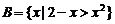
(1)求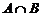 ;(2)若集合
;(2)若集合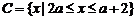 ,且
,且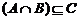 ,求实数
,求实数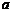 的取值范围.
的取值范围.
18(本小题12分)已知集合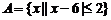 ,求函数
,求函数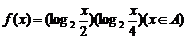 的值域.
的值域.
19(本小题12分)对于函数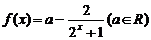
(1)是否存在实数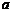 ,使得函数
,使得函数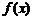 是奇函数,若存在求出
是奇函数,若存在求出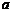 值,不存在说明理由;
值,不存在说明理由;
(2)判断函数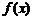 的单调性,并证明.
的单调性,并证明.
20(本小题12分)已知函数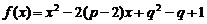 满足
满足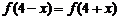
(1)求实数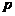 的值;(2)若在区间
的值;(2)若在区间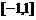 上至少存在一点
上至少存在一点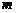 ,使
,使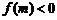 ,求实数
,求实数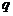 的范围.
的范围.
21(本小题12分)某企业打算购买工作服和手套,市场价为每套工作服53元,每副手套3元,该企业联系了两家商店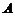 和
和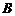 ,由于用货量大,这两家商店都给出了优惠条件:
,由于用货量大,这两家商店都给出了优惠条件:
商店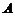 :买一赠一,买一套工作服,赠一副手套;
:买一赠一,买一套工作服,赠一副手套;
商店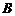 :打折,按总价的95%收款.
:打折,按总价的95%收款.
该企业需要工作服75套,手套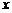 副(
副(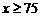 ),如果工作服与手套只能在一家购买,请你帮助老板选择在哪一家商店购买更省钱?
),如果工作服与手套只能在一家购买,请你帮助老板选择在哪一家商店购买更省钱?
22(本小题12分)已知二次函数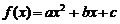
(1)若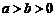 且
且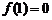 ,证明:函数
,证明:函数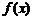 有两个零点;
有两个零点;
(2)证明:若对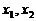 ,且
,且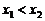 ,
,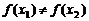 ,则方程
,则方程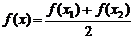 必有一实根在区间
必有一实根在区间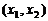 内;
内;
(3)在(1)的条件下,是否存在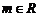 ,使
,使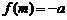 成立且
成立且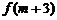 为正数?证明你的结论.
为正数?证明你的结论.
17(本小题10分)已知集合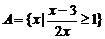 ,集合
,集合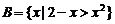
(1)求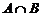 ;(2)若集合
;(2)若集合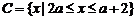 ,且
,且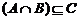 ,求实数
,求实数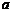 的取值范围.
的取值范围.
18(本小题12分)已知集合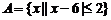 ,求函数
,求函数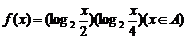 的值域.
的值域.
19(本小题12分)对于函数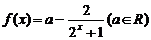
(1)是否存在实数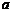 ,使得函数
,使得函数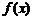 是奇函数,若存在求出
是奇函数,若存在求出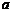 值,不存在说明理由;
值,不存在说明理由;
(2)判断函数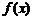 的单调性,并证明.
的单调性,并证明.
20(本小题12分)已知函数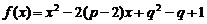 满足
满足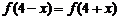
(1)求实数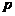 的值;(2)若在区间
的值;(2)若在区间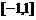 上至少存在一点
上至少存在一点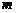 ,使
,使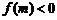 ,求实数
,求实数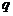 的范围.
的范围.
21(本小题12分)某企业打算购买工作服和手套,市场价为每套工作服53元,每副手套3元,该企业联系了两家商店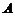 和
和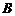 ,由于用货量大,这两家商店都给出了优惠条件:
,由于用货量大,这两家商店都给出了优惠条件:
商店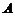 :买一赠一,买一套工作服,赠一副手套;
:买一赠一,买一套工作服,赠一副手套;
商店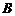 :打折,按总价的95%收款.
:打折,按总价的95%收款.
该企业需要工作服75套,手套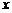 副(
副(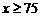 ),如果工作服与手套只能在一家购买,请你帮助老板选择在哪一家商店购买更省钱?
),如果工作服与手套只能在一家购买,请你帮助老板选择在哪一家商店购买更省钱?
22(本小题12分)已知二次函数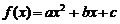
(1)若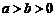 且
且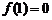 ,证明:函数
,证明:函数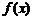 有两个零点;
有两个零点;
(2)证明:若对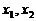 ,且
,且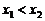 ,
,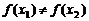 ,则方程
,则方程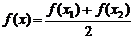 必有一实根在区间
必有一实根在区间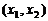 内;
内;
(3)在(1)的条件下,是否存在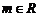 ,使
,使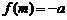 成立且
成立且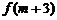 为正数?证明你的结论.
为正数?证明你的结论.
哈六中2013届高一上学期期中考试数学试题
满分150分 时间120分钟
16.函数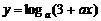 在
在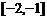 上是单调递增的,则实数
上是单调递增的,则实数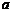 的范围是____________________
的范围是____________________
15.函数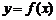 在
在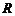 上是增函数,则函数
上是增函数,则函数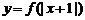 的单调减区间是____________________
的单调减区间是____________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com