
题目列表(包括答案和解析)
22.(本题满分10分)已知函数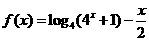 .
.
(Ⅰ)判断f(x)的奇偶性,并说明理由;
(Ⅱ)若方程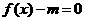 有解,求m的取值范围;
有解,求m的取值范围;
(Ⅲ)若函数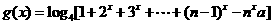 ,
,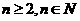 ,对任意
,对任意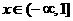 都有意义,求
都有意义,求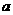 的取值范围.
的取值范围.
21.解:(1)SΔAEH=SΔCFG=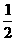 x2,SΔBEF=SΔDGH=
x2,SΔBEF=SΔDGH=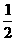 (a-x)(2-x). ……1分
(a-x)(2-x). ……1分
∴y=SABCD-2SΔAEH-2SΔBEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x. ……3分
由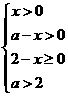 ,得
,得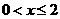
∴y=-2x2+(a+2)x,其定义域为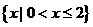 . ……4分
. ……4分
(2)当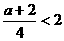 ,即a<6时,则x=
,即a<6时,则x=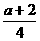 时,y取最大值
时,y取最大值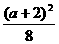 . ……6分
. ……6分
当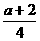 ≥2,即a≥6时,y=-2x2+(a+2)x,在
≥2,即a≥6时,y=-2x2+(a+2)x,在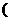 0,2]上是增函数,则x=2时,y取最大值2a-4 . ……8分
0,2]上是增函数,则x=2时,y取最大值2a-4 . ……8分
综上所述:当a<6时,AE=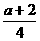 时,绿地面积取最大值
时,绿地面积取最大值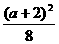 ;当a≥6时,AE=2时,绿地面积取最大值2a-4.
;当a≥6时,AE=2时,绿地面积取最大值2a-4.
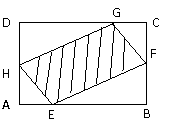
21.(本题满分8分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地,使其四个顶点分别落在矩形的四条边上,已知AB=a(a>2),BC=2,且AE=AH=CF=CG,设AE=x,绿地面积为y.
 (Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅰ)写出y关于x的函数关系式,并指出这个函数的定义域;
(Ⅱ)当AE为何值时,绿地面积最大?
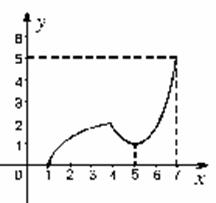
20.解:(Ⅰ)图像如右上图所示,此题需突出(1,0),
(4,2), (5,1), (7,5)四个点,并保留作图痕迹;(4分)
(Ⅱ)当1 x
x 4时,
4时,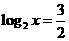 ,得
,得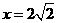 (5分);
(5分);
当4<x 7时,
7时,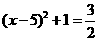 ,得
,得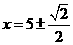 (7分);
(7分);
故函数g(x)=f(x)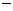
 的零点为
的零点为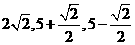 (8分).
(8分).
20. (本题满分8分)已知函数
(本题满分8分)已知函数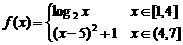 .
.
(Ⅰ)在给定的直角坐标系内画出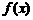 的图象;
的图象;
(Ⅱ)求函数g(x)=f(x)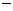
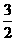 的零点.
的零点.
19、解:(Ⅰ) =,(2,+∞) (左端点可以闭) 2分
(Ⅱ) x=2时,ymin=4 4分
(Ⅲ)设0<x1<x2<2,则f(x1)-
f(x2)= 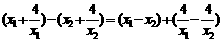
=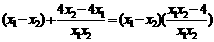 6分
6分
∵0<x1<x2<2 ∴x1-x2<0,0<x1x2<4 ∴x1x2-4<0
∴f(x1)-f(x2)>0 ∴f(x1)> f(x2)
∴f(x)在区间(0,2)上递减 8分
19.(本题满分8分)探究函数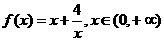 的最小值,并确定相应的x的值,列表如下:
的最小值,并确定相应的x的值,列表如下:
|
x |
… |
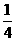 |
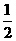 |
1 |
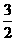 |
2 |
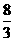 |
4 |
8 |
16 |
… |
|
y |
… |
16.25 |
8.5 |
5 |
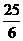 |
4 |
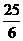 |
5 |
8.5 |
16.25 |
… |
请观察表中y值随x值变化的特点,完成下列问题:
(Ⅰ)若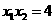 ,则
,则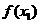
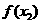 (请填写“>, =, <”号);若函数
(请填写“>, =, <”号);若函数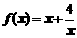 ,(x>0)在区间(0,2)上递减,则在 上递增;
,(x>0)在区间(0,2)上递减,则在 上递增;
(Ⅱ)当x= 时,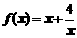 ,(x>0)的最小值为
;
,(x>0)的最小值为
;
(Ⅲ)试用定义证明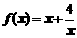 ,(x>0)在区间(0,2)上递减.
,(x>0)在区间(0,2)上递减.
18.解:(1)由不等式组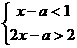 得
得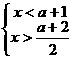 ,(2分)
,(2分)
当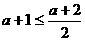 ,即
,即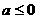 时
时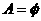 ,满足
,满足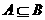 ;(4分)
;(4分)
当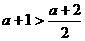 ,即
,即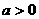 时
时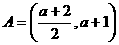 ,
,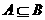 ,所以
,所以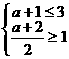 ,解得
,解得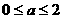 ,所以
,所以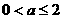 .(7分)
.(7分)
综述上面情况,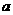 的取值范围是
的取值范围是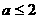 . ………… 8分
. ………… 8分
(注:如果漏空集未考虑,扣2分)
18.(本题满分8分)已知关于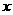 不等式组
不等式组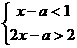 的解集为
的解集为 ,集合
,集合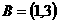 ,若
,若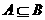 ,求a的取值范围.
,求a的取值范围.
17.解:(Ⅰ)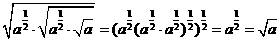 ;(3分)
;(3分)
(Ⅱ)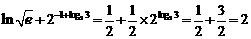 .(6分)
.(6分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com