
题目列表(包括答案和解析)
6、一个棱柱为正四棱柱的条件是( )
A、底面是正方形,有两个侧面垂直于底面
B、底面是正方形,有两个侧面是矩形 C、底面都是全等的矩形
D、底面是菱形,且有一个顶点处的三条棱两两垂直
5、已知α∩β=l,α⊥β,P∈α,P l,则下列命题中的假命题是( )
l,则下列命题中的假命题是( )
A、过P点且垂直于α的直线平行于β
B、过点P且垂直于l的平面垂直β
C、过点P且垂直于β的直线在α内
D、过点P且垂直于l的直线在α内
4、已知m、n表示两条直线,α、β表示两个平面,给出下列条件
①m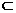 α,n
α,n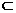 α,m∥β,n∥β ②m、n异面,且m⊥α,n⊥β
α,m∥β,n∥β ②m、n异面,且m⊥α,n⊥β
③m、n异面,且m∥α,m∥β,n∥α,n∥β
④m、n相交且都在α、β外,m∥α,m∥β,n∥α,n∥β
则其中能使α∥β的两个条件是 ( )
A、①和② B、②和③ C、③和④ D、①和④
3、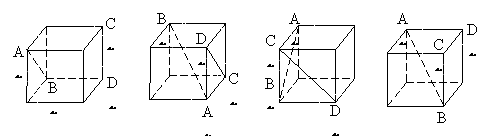 下列四个正方体中,能得出AB⊥CD的是 ( )
下列四个正方体中,能得出AB⊥CD的是 ( )
A B C D
2、已知两条异面直线a、b所成的角为60°,直线l与a、b所成的角均等于θ,则θ的取值范围是 ( )
A、[30°,90°] B、[30°,90°) C、(30°,60°] D、[60°,120°]
1、直线c与异面直线a、b都相交,直线d与a相交且与c平行,则d与b的位置关系是 ( )
A、相交 B、平行 C、异面 D、相交或异面
22.(14分) 解法一:
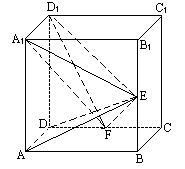
(Ⅰ)∵AC1是正方体,∴AD⊥面DC1. 又D1F面DC1, ∴AD⊥D1F.
(Ⅱ)取AB中点G,连结A1G,FG.因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,A1G∥D1F.
设A1G与AE相交于点H,则∠AHA1是AE与D1F所成的角,因为E是BB1的中点,所以Rt△A1AG≌Rt△ABE,∠GA1A=∠GAH,从而
∠AHA1=90°,即直线AE与D1F所成角为直角.
(Ⅲ)由(Ⅰ)知AD⊥D1F,由(Ⅱ)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED.又因为D1F面A1FD1,所以面AED⊥面A1FD1.
(Ⅳ)连结GE,GD1. ∵FG∥A1D1,∴FG∥面A1ED1, ∵AA1=2,
面积S△A1GE=S□ABB1A1-2S△A1AG--S△GBE=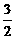
又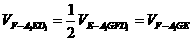
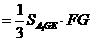
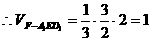
解法二:利用用向量求解
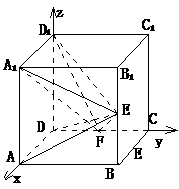
解析:设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,则D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A1(2,0,2),D1(0,0,2),
(I) ∵ 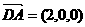 ,
,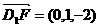 ,得
,得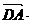
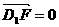 ,∴ AD⊥D1F;
,∴ AD⊥D1F;
(II)又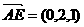 ,得
,得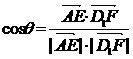
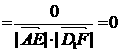
∴ AE与D1F所成的角为90°
(III) 由题意: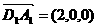 ,
,
设平面AED的法向量为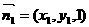 ,设平面A1FD1的法向量为
,设平面A1FD1的法向量为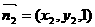 ,
,
 由
由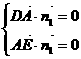
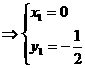
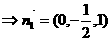
由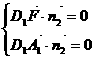
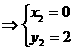
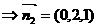
21.解:如图
(1)设 为
为 中点,连结
中点,连结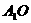

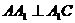 ,
,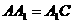
∴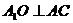
 平面
平面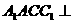 平面
平面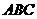 ,平面
,平面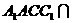 平面
平面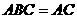 ,
,
∴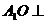 平面
平面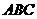 ,所以
,所以 为
为 与底面
与底面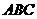 所成的角,大小为
所成的角,大小为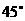 .
.
(2)设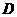 为
为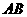 中点,连结
中点,连结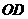 ,
,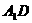

 为
为 中点,
中点,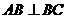
∴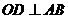
又
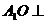 平面
平面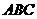
∴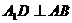 ,所以
,所以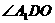 为
为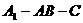 的平面角
的平面角
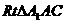 中,
中,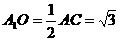 ,
,
又因为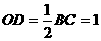 ,所以
,所以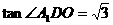 ,从而得
,从而得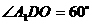 .
.
(3)设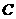 点到平面
点到平面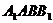 的距离为
的距离为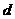
在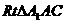 中,
中,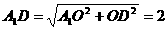 ,同理可得
,同理可得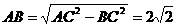
所以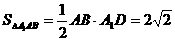 ,
,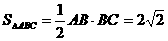
由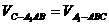 ,即
,即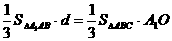 ,得
,得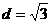 .
.
20.(12分)解:①60°;
②连SM,CM, ∵∠SBA=45° ∴SM⊥AB, 又CS⊥AB, ∴AB⊥面CSM.
过S作CM的垂线SN,垂足为N,则SN⊥CM,SN⊥AB,∴SN⊥面ABC.
 ∠SCN为所求的线面角,设SB=1 则不难计算 CS=
∠SCN为所求的线面角,设SB=1 则不难计算 CS=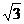 ,SM=
,SM=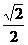 ,CM=
,CM=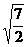 sin∠SCM=
sin∠SCM=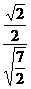 =
=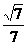 .
.

19.(12分) 如图,连结EG、FG、EF、BD、AC.EF、BD分别交AC于H、O. 因为ABCD是正方形,E、F分别为AB和AD的中点,故EF∥BD,H为AO的中点.
BD不在平面EFG上.否则,平面EFG和平面ABCD重合,从而点G在平面的ABCD上,与题设矛盾.
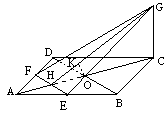 由直线和平面平行的判定定理知BD∥平面EFG,
由直线和平面平行的判定定理知BD∥平面EFG,
所以BD和平面EFG的距离就是点B到平面EFG的距离.
∵BD⊥AC ∴EF⊥HC. ∵GC⊥平面ABCD, ∴EF⊥GC,
∴EF⊥平面HCG. ∴平面EFG⊥平面HCG,HG是这两个垂直平面的交线.
作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com