14.某班50人参加考试。请设计一个算法统计出80分以上的人数，并画出程序框图。

13.请编写出一个“求满足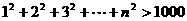的n最小值”的程序。

22．(本小题满分14分)

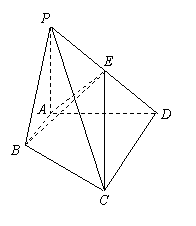如图，四棱锥P-ABCD的底面是直角梯形，ÐCDA=90°，AB∥CD，AB=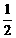CD，

PA^面ABCD，E为PD的中点．

(1) 证明：AE∥平面PBC；

(2) 当二面角P-CD-B为45°时，

证明：平面PBC^平面PCD；

(3) 在(2)的条件下，若AD=2，CD=4，

求三棱锥C-PBE的体积．

21．(本小题满分12分)

甲、乙两人进行乒乓球比赛，采用“五局三胜制”，即五局中先胜三局者为胜．若每局比赛甲获胜的概率都是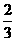，乙获胜的概率都是．

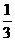求：(1)比赛以甲三胜一负而结束的概率；

(2)比赛以乙获胜而结束的概率．

20．(本小题满分12分)

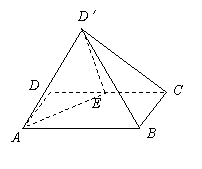已知E是矩形ABCD边CD的中点，且CD=2，BC=1．现沿AE将△DAE折起至△D′AE，使得D′到B、C两点的距离相等．

(1) 求证：平面D′AE⊥平面ABCE；

(2) 求二面角D′-BC-A的大小；

(3) 求点A到平面D′BC的距离．

19．(本小题满分12分)

如右图，用A、B、C、D四类不同的元件连接成系统N，

当元件A正常工作且元件B、C都正常工作，或当元件A

正常工作且元件D正常工作时，系统N正常工作．已知

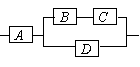A、B、C、D正常工作的概率依次为，，，．

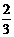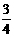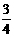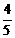(1) 求元件A、B、C都正常工作的概率；

(2) 求系统N正常工作的概率．

18．(本小题满分12分)

如图，正三角形ABC与直角三角形BCD成直二面角，且ÐBCD=90°，ÐCBD=30°．

(1)求证：AB^CD；

(2)求二面角D-AB-C的大小；

(3)求异面直线AC和BD所成的角．

17．(本小题满分12分)

已知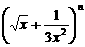的展开式中第五项的二项式系数与第三项的二项式系数的比

是14∶3，求展开式中不含x的项．

13．　　　　　 　14．　　　　　 　　15．　　　　　　 　16．　　　　　　

16．给出下列四个命题：

① 若l∥a，则l平行于a内的每一条直线；

② 空间中，到定点的距离等于定长的点的轨迹是圆；

③ 曲线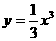在点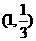处的切线与直线x+y-3=0互相垂直；

④ 如果一个简单多面体的所有面都是四边形，那么F=V–2(其中F是面数，V是顶点数)．

其中正确命题的序号是：　 　　　　　　．

高二数学测试卷