
题目列表(包括答案和解析)
2、已知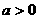 ,函数
,函数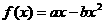 ;
;
(1)当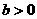 时,若对任意
时,若对任意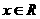 都有
都有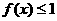 ,证明:
,证明: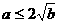 ;
;
(2)当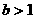 时,证:对任意
时,证:对任意 ,
,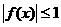 的充要条件是
的充要条件是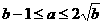 ;
;
(3)当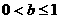 时,讨论:对任意
时,讨论:对任意 ,
,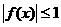 的充要条件。
的充要条件。
2、性质的应用。
[例题]
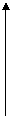 例1、(1)设函数
例1、(1)设函数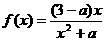 的图象如图所示,则
的图象如图所示,则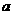 的范围是()
的范围是()
 A、
A、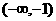 B、
B、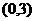 C、
C、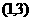 D、
D、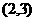
 (2 )函数
(2 )函数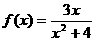 的值域为
的值域为
例2、
知函数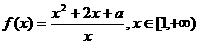 ,
,
(1)当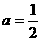 时,求函数
时,求函数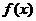 的最小值;
的最小值;
(2)若对任意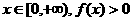 横成立,试求实数
横成立,试求实数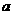 的取值范围。
的取值范围。
例3、已知函数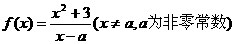
(1)解不等式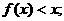
(2)设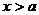 时,
时,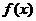 的最小值为6,求
的最小值为6,求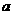 的值。
的值。
例4、设计一幅宣传画,要求画面面积为4840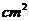 ,画面的宽与高的比为
,画面的宽与高的比为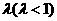 ,画面的上、下各留8
,画面的上、下各留8 空白,左右各留5
空白,左右各留5 空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求
空白,怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?如果要求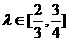 ,那么
,那么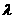 为何值时,能使宣传画所用纸张面积最小?
为何值时,能使宣传画所用纸张面积最小?
练习:1、设定义域为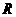 的奇函数
的奇函数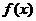 是增函数,若当
是增函数,若当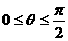 时,
时,
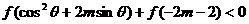
求 的取值范围。
的取值范围。
1、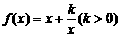 的性质和图象。
的性质和图象。
2、定义在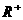 上的函数
上的函数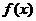 ,对任意的
,对任意的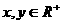 都
都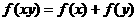 ,当且仅当
,当且仅当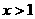 时,
时,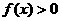 成立;
成立;
(1) 设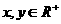 ,求证:
,求证: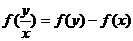 ; (2)设
; (2)设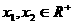 ,若
,若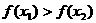 比较
比较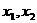 的大小;
的大小;
(3)解不等式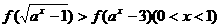
专题四:函数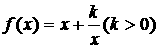
[基本知识]
4、设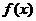 是定义在R上的偶函数,其图象关于
是定义在R上的偶函数,其图象关于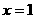 直线对称,对任意
直线对称,对任意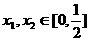 ,都有
,都有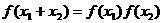 ,且
,且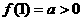 ;
;
(I)求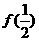 ,
,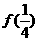 (II)证明
(II)证明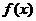 是周期函数;
是周期函数;
(III)记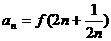 ,求
,求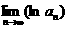 。
。
练习:1、已知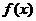 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且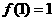 ,若
,若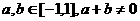 有
有
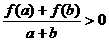 ;(I)证明
;(I)证明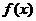 是[-1,1]单调函数;(II)解不等式
是[-1,1]单调函数;(II)解不等式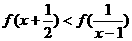 。
。
3、已知函数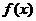 的定义域为
的定义域为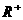 ,且对任意
,且对任意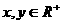 ,恒有
,恒有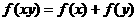 ;
;
(1)证明:当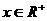 时,
时,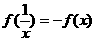 ;
;
(2)若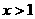 时,恒有
时,恒有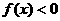 成立,则
成立,则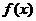 必有反函数;
必有反函数;
(3)设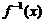 是的反函数,则
是的反函数,则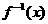 在其定义域内恒有
在其定义域内恒有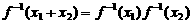 成立。
成立。
2、设函数的定义域为R,并满足条件:存在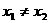 ,使得
,使得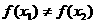 ,又对任何
,又对任何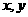
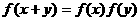 成立,证明:
成立,证明:
(1)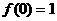 ; (2)
; (2)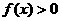 对任何
对任何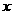 都成立。
都成立。
1、(1)设函数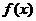 定义在实数集上,函数
定义在实数集上,函数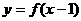 与
与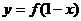 的图象关于()
的图象关于()
A、直线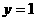 对称 B、直线
对称 B、直线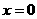 对称 C、直线
对称 C、直线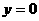 对称D、直线
对称D、直线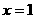 对称
对称
 (2)设
(2)设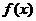 是R上的奇函数,则函数
是R上的奇函数,则函数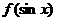 是R上的 函数;
是R上的 函数;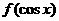 是R上的
函数。
是R上的
函数。
 (3)如果奇函数在
(3)如果奇函数在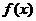 在区间[3,7]上是增函数,那么
在区间[3,7]上是增函数,那么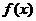 在区间[-7,-3]上是()
在区间[-7,-3]上是()
A、增函数且最小值为-5 B、增函数且最大值为-5
C、减函数且最小值为-5 D、减函数且最大值为-5
(4)设函数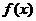 定义域为R且满足:
定义域为R且满足:
1)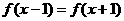 ;2)
;2)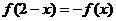 ;3)
;3)
3)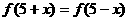 且
且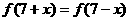 ;4)
;4)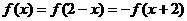
(5)设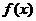 是R上的奇函数,
是R上的奇函数,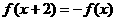 ,当
,当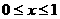 时,
时,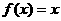 ,则
,则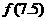 等于 ()
等于 ()
A、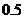 B、
B、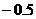 C、
C、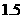 D、
D、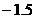
3、 抽象函数的求解方法。
[例题]
2、 抽象函数的性质。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com