
题目列表(包括答案和解析)
7.三条相交直线最多可以确定( ).
A.一个平面 B.两个平面 C.三个平面 D.四个平面
6.下列命题中正确的是( ).
A.经过三点确定一个平面 B.经过一条直线和一个点确定一个平面
C.经过两条直线确定一个平面 D.两两相交且不共点的三条直线确定一个平面
5.用符号表示下列各命题的结论:
(1)若A∈a,A∈b,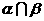 =l,则______________;
=l,则______________;
(2)若A∈a,B∈a,A∈b,B∈b,则___________;(其中a、b 不重合)
(3)若a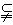 a,a
a,a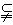 b,则___________;(其中a、b不重合)
b,则___________;(其中a、b不重合)
(4)若AB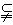 a,C∈AB,则___________;
a,C∈AB,则___________;
(5)若PQ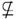 a,P∈a,则___________.
a,P∈a,则___________.
4.填空:
(1)要判断一条直线在某一平面内,只要判断这条直线上的_________个点在此平面内.
(2)要寻找两个平面的公共点,应该在这两个平面的__________上去找.
(3)“确定一个平面”的含义是__________________.
3.用符号表示下列语句,并画出图形:
(1)直线l经过平面a 内两点A、B;
(2)直线l在平面a 外,且过平面a 内一点P;
(3)直线l在平面a 内,又在平面b 内;
(4)直线l是平面a与b的交线,平面a内一条直线m与l平行.
2.填空:(平面ABEF记作a ,平面ABCD记作b ,依图9-1填写)
(1)A∈a,B_____ a,E_____ a,C_____ a ,D_____a ;
(2)A∈b,B_____ b,C_____ b,D_____ b,E_____b,F_____ b;
(3)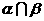 =_________;
=_________;
(4)AB______ a ,AB_____ b,CD_____ a ,CD_____ b,AE_____ b,AE_____ b.
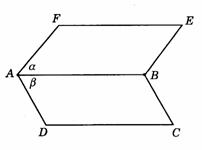
图9-1
1.判断下列命题是否正确,并说明理由.
(1)一个平面的面积是 ;
;
(2)平面内的一条线段把这平面分成两部分;
(3)两个平面a 和b 是可能有且只有一个公共点的;
(4)四边形一定是平面图形;
(5)同一平面内不重合的两条直线最多有一个交点;
(6)如果一条直线l在平面a 外,那么这条直线与平面是没有公共点.
10.设等腰三角形OAB的顶角为2θ,高为h
(1)△OAB内有一动点P到三边OA、OB,AB的距离分别为|PD|、|PF|、|PE|,且满足关系:
|PD|·|PF|=|PE|2,求P点的轨迹.
(2)在上述轨迹中定出P点的坐标,使得|PD|+|PE|=|PF|
[知识探究学习]
如图所示是某防空部队进行射击训练时在平面直角坐标系中的示意图,在地面O、A两个观点测得空中固定目标C的仰角分别为α和β,OA=1千米,tanα=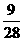 ,tanβ=
,tanβ=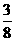 ,位于O点正上方
,位于O点正上方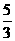 千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
千米的D点处的直升飞机向目标C发射防空导弹,该导弹运行与地面最大高度为3千米,相应水平距离为4千米(即图中E点),不考虑空气阻力,导弹飞行轨道为一抛物线,那么按轨道运行的导弹能否击中目标C?说明理由.
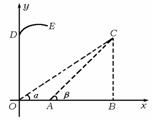
解:能否击中C点,关键是看一下C点是否在导弹飞行的轨迹上,因此应选求C点坐标,然后求轨迹的方程,再验证该点是否满足轨迹方程.
设抛物线为y=a(x-4)2+3,由抛物线过点(0, 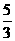 ),求得a=-
),求得a=-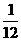 .
.
所以 y=-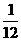 (x-4)2+3
(x-4)2+3
=-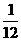 x2+
x2+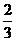 x+
x+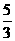 .
.
设C点坐标为(x0,y0),过C作CB⊥Ox于B,
tanα=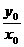 =
=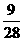 ,tanβ=
,tanβ=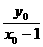 =
=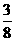 .
.
则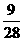 x0=
x0=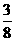 (x0-1).
(x0-1).
解得x0=7,求出y0=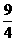 .
.
即C点坐标为(7,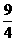 ),经计算
),经计算
-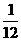 x02+
x02+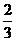 x0+
x0+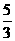 =-
=-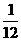 ×72+
×72+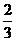 ×7+
×7+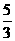 =
=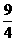 .
.
所以C点在抛物线上.
故依轨道运行的导弹可以击中目标C.
9.求两直线l1:x-3my+3=0,l2,3mx+y+9m=0的交点的轨迹,并画出轨迹的图形.
8.已知关于x,y的方程x2-4xy+my2-x+(3m-10)y-2=0表示两条直线,则m= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com