
题目列表(包括答案和解析)
1, 方程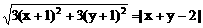 表示的曲线是
表示的曲线是
A、 椭圆 B、双曲线 C、抛物线 D、不能确定
2,方程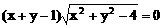 的曲线形状是
的曲线形状是
A、圆 B、直线 C、圆或直线 D、圆或两射线
3,以抛物线y2=2px(p>0)的焦半径|PF|为直径的圆与y轴位置关系是
A、相交 B、相切 C、相离 D、以上三种均有可能
4,已知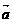 =(2,-1,3),
=(2,-1,3),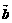 =(-1,4,-2),
=(-1,4,-2),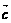 =(7,5,λ),若
=(7,5,λ),若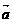 、
、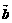 、
、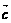 三向量共
三向量共
面,则实数λ等于 ( )
A.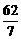 B.
B.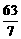 C.
C.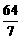 D.
D.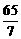
5,直三棱柱ABC-A1B1C1中,若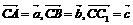 , 则
, 则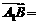 ( )
( )
A.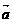 +
+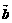 -
-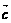 B.
B.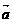 -
-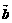 +
+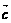 C.-
C.-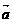 +
+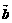 +
+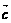 D.-
D.-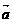 +
+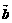 -
-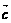
6,已知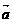 +
+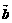 +
+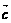 =
=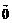 ,|
,|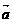 |=2,|
|=2,|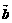 |=3,|
|=3,|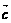 |=
|=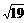 ,则向量
,则向量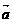 与
与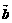 之间的夹角
之间的夹角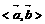 为( )
为( )
A.30° B.45° C.60° D.以上都不对
7,已知△ABC的三个顶点为A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的
中线长为 ( )
A.2 B.3 C.4 D.5
8,已知双曲线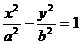 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
A.( 1,2) B. (1,2) C.[2,+∞] D.(2,+∞)
9,已知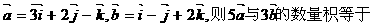 ( )
( )
A.-15 B.-5 C.-3 D.-1
10,已知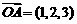 ,
,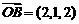 ,
,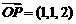 ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当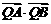
取得最小值时,点Q的坐标为 ( )
A.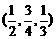 B.
B.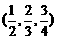 C.
C.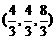 D.
D.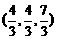
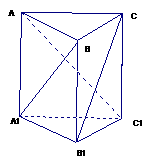
22.(10分)如图, 已知三棱柱ABC-A1B1C1中,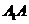 、B1B、C1C垂直底面,有下列三个条件:(1)
、B1B、C1C垂直底面,有下列三个条件:(1)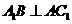 , (2 )
, (2 ) 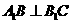 (3)
(3) 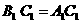 , 问利用 (1),(2),(3)可以构造出多少个正确的命题,请写出这些正确的命题,并选择其中一个正确命题加以证明。
, 问利用 (1),(2),(3)可以构造出多少个正确的命题,请写出这些正确的命题,并选择其中一个正确命题加以证明。
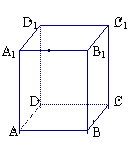
21.(10分)长方体ABCD-A1B1C1D1中AB=BC=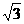 ,AA1=3,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
,AA1=3,点E,F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
①求证:A1C⊥面AEF; ②求二面角A-EF-B的大小;③点B1到面AEF的距离;下
20. (10分)
(10分)
(文科做)求证:空间四边形的两条对角线是异面直线。
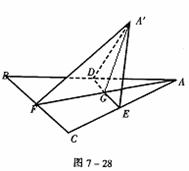
(理科做)已知边长为a的正三角形ABC的中线AF与中位线DE相交于G(如图7-28),将此三角形沿DE折成二面角A′-DE-B。(1).求证:平面A′GF⊥平面BCED;(2).当二面角A′-DE-B为多大时,异面直线A′E与BD互相垂直?证明你的结论。
18.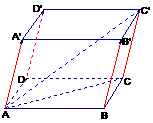 (8分) 已知平行六面体
(8分) 已知平行六面体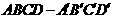 中,
中,
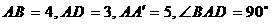 ,
,
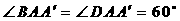 ,求
,求 的长
的长
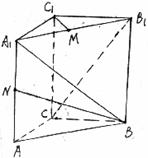 19.(10分)如图,三棱柱ABC-A1B1C1中,
19.(10分)如图,三棱柱ABC-A1B1C1中,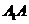 、B1B、C1C垂直底面,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点,
、B1B、C1C垂直底面,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点,
(1)求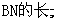
(2)异面直线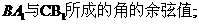
(3)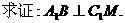
17. (8分)已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,且EH∥FG.求证:EH∥BD.
(8分)已知E、F、G、H为空间四边形ABCD的边AB、BC、CD、DA上的点,且EH∥FG.求证:EH∥BD.
16.将边长为2,锐角为60°的菱形ABCD沿较短对角线BD折成四面体ABCD,点E、F分别为AC、BD的中点,则下列命题中正确的是 。(将正确的命题序号全填上)
①EF∥AB ②EF是异面直线AC与BD的公垂线
③当四面体ABCD的体积最大时,AC=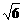 ④AC垂直于截面BDE
④AC垂直于截面BDE
15.已知A(0,2,3),B(-2,1,6),C(1,-1,5),若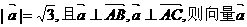 的坐标为 .
的坐标为 .
14.若A(m+1,n-1,3),B(2m,n,m-2n),c(m+3,n-3,9)三点共线,则m+n= .
13.正方体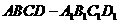 中,平面
中,平面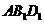 和平面
和平面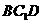 的位置关系为
的位置关系为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com