
题目列表(包括答案和解析)
1、对草莓、橙子、桃子、苹果、梨等水果进行分类时,可选取的指标为( )
A)只能以维生素的含量作为指标 B)只能以形状作为指标
C)只能以颜色作为指标 D)以上都可以
(二)填空题
6、如果球的半径扩大为原来的n倍,则球的大圆周长扩大为原来的______倍,球的表面积扩大为原来的______倍,球的体积扩大为原来的______倍。
7、过球面上不经过球心的两点所作截面圆中,面积最大的圆是________,面积最小的圆是__________。
8、长方体共顶点的三个侧面面积分别为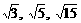 ,则它的外接球的表面积为__________。
,则它的外接球的表面积为__________。
9、设地球半径为R,在北纬600的圈上有甲、乙两地,它们纬度圈上的弧长等于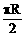 ,那么甲、乙两地球面距离为__________。
,那么甲、乙两地球面距离为__________。
10、由半径为R的球面上一点P作球的两两互相垂直的三条弦PA、PB、PC,则PA2+PB2+PC2=__________。
 (三)解答题
(三)解答题
11、设地球半径为R,A地在东经300的赤道上,B地在北纬450,东经1200处,求A、B两地球面的距离。
12、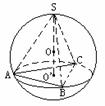 正三棱锥高为1,底面边长为
正三棱锥高为1,底面边长为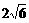 ,内有一个球与四个面都相切,如图
,内有一个球与四个面都相切,如图
(1) 求棱锥的全面积;
(2) 求球的半径。
13、正三棱锥内接于半径为R的球,如果它的高与侧棱所成的角等于α,求棱锥体积。
14、已知AB为球O的直径,C、D是球面上两点,D又在以BC为直径的小圆上,设此小圆所在平面为α
(1)
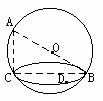 求证:平面ABC⊥α;
求证:平面ABC⊥α;
(2)设AB与α所成角为θ,过球半径OD且垂直于α的截面截BC弦于E,求△OED与经过O、D的截面面积之比,并求θ为何值时,这面积之比最大。
(一)选择题
1、 棱长为a的正方体外接球的表面积是
A、πa2 B、2πa2 C、3πa2 D、4πa2
2、A、B为球面上相异两点,则过A、B可作大圆个数
A、0个 B、只有一个 C、无穷多个 D、以上都不对
3、若球的大圆面积扩大为原来的2倍,则球的体积比原来增加
A、2倍
B、4倍
C、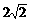 倍 D、
倍 D、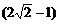 倍
倍
4、两个球的体积之比为8∶27,那么这两个球的表面积之比为
A、2∶3
B、4∶9
C、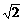 ∶
∶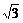 D、
D、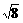 ∶
∶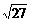
5、表面积为Q的多面体的每一个面都外切于半径为3的一个球,则这个多面体体积为
A、Q
B、3Q
C、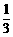 Q
D、无法求解
Q
D、无法求解
例1、 四棱锥A-BCDE中,AD⊥平面BCDE,AC⊥BC,AE⊥BE,
(1)求证A、B、C、D、E五点都在以AB为直径的同一球面上;
(2)若∠CBE=900,CE=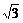 ,AD=1,求B、D两点的球面距离。
,AD=1,求B、D两点的球面距离。
解题思路分析:
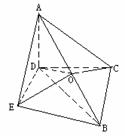 (1)设AB中点为O,则只需证明OA=OB=OC=OD=OE,其途径通常有全等三角形或等量代换。本题用等量代换。
(1)设AB中点为O,则只需证明OA=OB=OC=OD=OE,其途径通常有全等三角形或等量代换。本题用等量代换。
设AB中点为O,则OA=OB=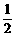 AB
AB
∵ AD⊥平面BCDE
∴ AD⊥DB
∴ DO=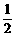 AB
AB
∵ AC⊥BC,AE⊥EB
∴
EO=CO=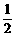 AB
AB
∴ OA=OB=OC=OD=OE=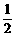 AB
AB
即A、B、C、D、E五点都在以AB为直径的同一球面上
(2)根据球面距离的定义,只需求出球的半径R及∠BOD的大小即可。下从分析图形A-BCDE的性质着手。
∵ AD⊥平面BCDE
∴ DE、DC分别为AE、AC在平面BCDE上的射影
∵ BE⊥EA,BC⊥CA
∴ BE⊥ED,BC⊥CD
又∠CBE=900
∴ BCDE为矩形
∴
BD=EC=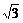
∴ AB=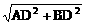 =2
=2
∴ 球半径R=1
△ BOD中,BO=OD=1,BD=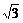
∴ cos∠BOD=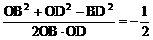
∴ ∠BOD=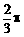
∴ B、D两点球面距离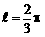
例2、有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体各条棱都相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比及体积之比。
解题思路分析:
因球的表面积及体积与球的半径有关,故求出三个球的半径之间关系即可。将正方体的棱长作为基本元素,以此找出三个半径的关系式。
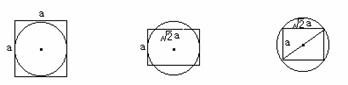 设正方体棱长为a,三个球的依次为R1、R2、R3,分别作出过球的球心的截面,得如图所示三种组合体的截面图。
设正方体棱长为a,三个球的依次为R1、R2、R3,分别作出过球的球心的截面,得如图所示三种组合体的截面图。
2R1=a,R1=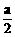
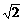 a=2R2,R2=
a=2R2,R2=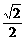 a
a 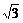 a=2R3,R3=
a=2R3,R3=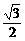 a
a
∴ R1∶R2∶R3=1∶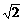 ∶
∶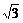
∴ S1∶S2∶S3=R12∶R22∶R32=1∶2∶3
V1∶V2∶V3=R13∶R23∶R33=1∶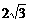 ∶
∶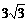
评注:本题通过作截面图,将立体几何问题转化为平面几何问题,是立体几何的重要思想方法之一。对于这类组合体,通常作出过球心的截面,然后紧抓球心及半径两个要素,找位置关系或数量关系。
例3、A、B、C为半径为1的球面上的三点,B、C两点的球面距离为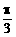 ,点A与B、C两点间的球面距离均为
,点A与B、C两点间的球面距离均为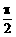 ,设球心为O,求:(1)∠BOC、∠AOB的大小;(2)球心到截面ABC的距离。
,设球心为O,求:(1)∠BOC、∠AOB的大小;(2)球心到截面ABC的距离。
解题思路分析:
从转化球面距离着手
(1)
由球面距离定义可知,∠BOC=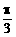 ,∠AOB=∠AOC=
,∠AOB=∠AOC=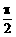 ;
;
(2) 法一:利用截面性质,求出△ABC的外接圆半径r即可
∵ BC=1,AC=AB=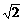
∴ cos∠BAC=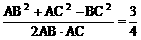
∴ sin∠BAC=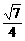
设△ABC外接圆半径为r,则由正弦定理
2r=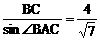
∴ r=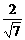
∴ 球心到截面ABC的距离为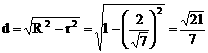
法二:一般说,立体几何的解题习惯是将点、线、面置于某一几何体中,充分利用几何体的有关性质解决这些点、线、面的问题。因此本题可考虑O、A、B、C四点构成的四面体
∵ OA⊥OB,OA⊥OC
∴ OA⊥平面OBC,如图
为了确定O在平面ABC上的射影,应先找到平面ABC的垂面(辅助平面)
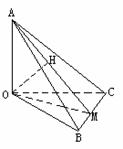 取BC中点M,则OM⊥BC
取BC中点M,则OM⊥BC
∴ BC⊥平面OAM
∴ 平面OAM⊥平面ABC
在△OAM内作OH⊥AM,H为垂足,则OH⊥平面ABC
∴ OH长度就是点O到平面ABC的距离
∵ OA=1,OM=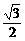
∴ AM=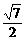
由OA·OM=AM·OH得:OH=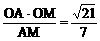
法三:在法二图形的基础上,也可用等积法求点O到平面ABC的距离
设O到平面ABC的距离为x,则
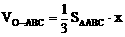
又 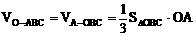
∴ 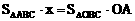
求得:S△ABC、S△OBC、OA后代入上式,求得x=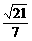
这种方法的优越性在于不需要作出O在平面ABC上的射影
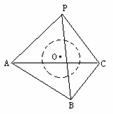
例4、三棱锥P-ABC中,PA⊥平面ABC,∠ABC=900,求这个三棱锥外接球球心的位置。
解题思路分析:
为了确定球心(点)的位置,可将它转化为某两条直线的公共点。那么球心在哪条直线上呢?
根据球的截面小圆的性质,球心在过截面圆的圆心且与截面圆垂直的直线上。
如图:∵ ∠ABC=900
∴ △ABC的外接圆圆心为AC中点O1,在△PAC内作O1M∥PA,则O1M⊥平面ABC
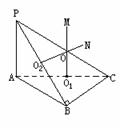 ∴ 球心O在直线O1M上
∴ 球心O在直线O1M上
∵ PA⊥平面ABC
∴ PA⊥BC
又BC⊥BA
∴ CB⊥平面PAB
∵ ∠PAB=900
∴ △PAB的外接圆圆心为PB中点O2,在△PBC内作O2N⊥CB,则O2N⊥平面PAB
∴ 球心O在直线O2N上
∵ O1M、O2N均与直线PC相交且交点O为PC中点
∴ O1M∩O2M=0
∴ O为三棱锥P-ABC外接球的球心
例5、已知球的两个平行截面的面积分别为5π和8π,且相距为1,求球的体积。
 解题思路分析:
解题思路分析:
利用解方程思想与球的半径R
这里还需要对两截面是在球心O的同侧还是异侧进行讨论
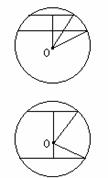
当两截面在球心O的同侧时,作出截面大圆,如图
则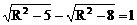
解之得R=3
当两截面在球心O的两侧时
则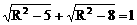 ,无解
,无解
∴ 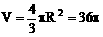
(三)解答题
16、四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,A1B=A1D,求证:(1)对角面AA1C1C⊥截面A1BD;(2)对角面D1DBB1是矩形。
17、正四棱柱ABCD-A1B1C1D1中,A1B与对角面A1B1CD所成角为300,求证:此四棱柱为正方体。
18、正四棱锥棱长均为a,(1)求侧面与底面所成角α;(2)若相邻两侧面所成角为β,求证:β=2α。
19、正三棱锥的侧棱等于10cm,侧面积等于144cm2,求棱锥的底面边长和斜高。
20、斜三棱柱ABC-A1B1C1的底面△ABC中,AB=AC=10,BC=12,A1到A、B、C三点的距离都相等,且AA1=13,求斜三棱柱的侧面积。
第8讲 球
(二)填空题
11、正四棱柱的一个侧面面积为S,则它的对角面面积是__________。
12、正n棱柱每相邻两个侧面所成二面角度数为__________。
13、长方体对角线长为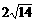 ,长、宽、高的比为3∶2∶1,则长方体全面积为________。
,长、宽、高的比为3∶2∶1,则长方体全面积为________。
14、正六棱柱的高为5cm,最长对角线为13cm,它的侧面积是__________。
15、一个正棱锥的一个侧面与底面所成角是θ,底面积Q,则它的侧面积是________。
(一) 选择题
1、 斜四棱柱侧面最多可有几个面是矩形
A、 0个 B、1个 C、2个 D、3个
2、 正方体的体对角线长为x,其体对角线长是
A、
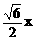 B、
B、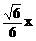 C、
C、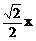 D、
D、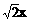
3、
若长方体的三个面的面积分别是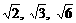 ,则长方体对角线长为
,则长方体对角线长为
A、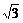 B、
B、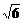 C、
C、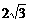 D、
D、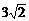
4、 下列命题正确的是
A、四棱柱是平行六面体 B、直平行六面体是长方体
C、六个面都是矩形的六面体是长方体 D、底面是矩形的四棱柱是长方体
5、 下列命题正确的是
A、 底面是正多边形的棱锥是正棱锥
B、 侧面与底面所成角都相等的棱锥是正棱锥
C、 棱锥的高可以等于它的一条侧棱长
D、 棱锥的高一定在棱锥内部
6、三棱锥S-ABC的三条侧棱两两垂直,SA=1,SB=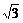 ,SC=
,SC=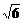 ,则底面内∠ABC等于
,则底面内∠ABC等于
A、300 B、450 C、600 D、1200
7、在四棱锥的四个侧面中,直角三角形最多可有
A、1个 B、2个 C、3个 D、4个
8、正方体ABCD-A1B1C1D1的表面积为S1,以A1、B、C1、D为顶点的四面体的表面积为S2,则S1∶S2等于
A、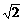 B、
B、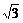 C、
C、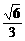 D、
D、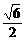
9、若正棱锥的底面边长为侧棱长相等,则该棱锥一定不是
A、三棱锥 B、四棱锥 C、五棱锥 D、六棱锥
10、棱锥的一个平行于底面的截面把棱锥的高分成1∶2(从顶点到截面与从截面到底面),那么这个截面把棱锥的侧面分成两部分的面积之比等于
A、1∶2 B、1∶4 C、1∶9 D、1∶8
例1、已知直三棱柱ABC-A1B1C1中,∠ACB=900,∠BAC=300,BC=1,AA1=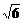 ,M为CC1中点,求证:AB1⊥A1M。
,M为CC1中点,求证:AB1⊥A1M。
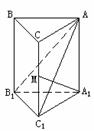 解题思路分析:
解题思路分析:
因结论是线线垂直,可考虑用三垂线定理或逆定理
∵ ∠ACB=900
∴ ∠A1C1B1=900
即B1C1⊥C1A1
又由CC1⊥平面A1B1C1得:CC1⊥B1C1
∴ B1C1⊥平面AA1C1C
∴ AC1为AB1在平面AA1C1C的射影
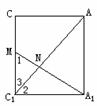 由三垂线定理,下证AC1⊥A1M即可
由三垂线定理,下证AC1⊥A1M即可
在矩形AA1C1C中,AC=A1C1=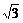 ,AA1=CC1=
,AA1=CC1=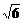
∵ 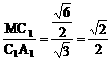 ,
,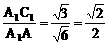
∴ 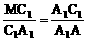
∴ Rt△A1C1M∽Rt△AA1C1
∴ ∠1=∠2
又∠2+∠3=900
∴ ∠1+∠3=900
∴ AC1⊥A1M
∴ AB1⊥A1M
评注:利用三垂线定理的关键是找到基本面后找平面的垂线
例2、正三棱柱ABC-A1B1C1的底面边长为a,在侧棱BB1上截取BD=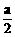 ,在侧棱CC1上截取CE=a,过A、D、E作棱柱的截面ADE
,在侧棱CC1上截取CE=a,过A、D、E作棱柱的截面ADE
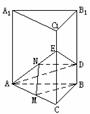 (1)求△ADE的面积;(2)求证:平面ADE⊥平面ACC1A1。
(1)求△ADE的面积;(2)求证:平面ADE⊥平面ACC1A1。
解题思路分析:
(1) 分别在三个侧面内求出△ADE的边长
AE=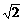 a,AD=
a,AD=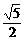 a,DE=
a,DE=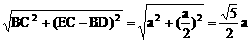
∴ 截面ADE为等腰三角形
S=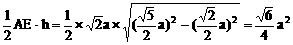
(2)∵ 底面ABC⊥侧面AA1C1C
∴ △ABC边AC上的高BM⊥侧面AA1C1C
下设法把BM平移到平面AED中去
取AE中点N,连MN、DN
∵ MN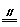
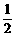 EC,BD
EC,BD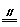
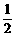 EC
EC
∴ MN BD
BD
∴ DN∥BM
∴ DN⊥平面AA1C1C
∴ 平面ADE⊥平面AA1C1C
评注:解决第(2)问题的方法是证明面面垂直的一种典型途径。第一步先找到其中一个平面的垂线,第二步将直线平移到另一个平面中去。实际上,第二步就是要证明线面平行,如本题BM∥平面ADE。根据前面介绍的用线面平行的判定定理证明线面平行的方法,只要过BM作一平面与平面ADE相交,则BM必和交线平行,这里构造了辅助平面BDNM。
本题也可作出二面角的平面角,证明其大小为900
例3、斜三棱柱ABC-A1B1C1中,底面是边长为4cm的正三角形,侧棱AA1与底面两边AB、AC均成600的角,AA1=7
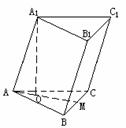 (1)求证:AA1⊥BC;(2)求斜三棱柱ABC-A1B1C1的全面积;(3)求斜三棱柱ABC-A1B1C1的体积;(4)求AA1到侧面BB1C1C的距离。
(1)求证:AA1⊥BC;(2)求斜三棱柱ABC-A1B1C1的全面积;(3)求斜三棱柱ABC-A1B1C1的体积;(4)求AA1到侧面BB1C1C的距离。
解题思路分析:
(1) 设A1在平面ABC上的射影为0
∵ ∠A1AB=∠A1AC
∴ O在∠BAC的平行线AM上
∵ △ABC为正三角形
∴ AM⊥BC
又AM为A1A在平面ABC上的射影
∴ A1A⊥BC
(2)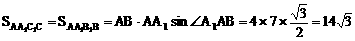
∵ B1B∥A1A
∴ B1B⊥BC,即侧面BB1C1C为矩形
∴ 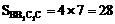
又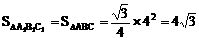
∴ S全=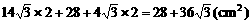
(3)∵ cos∠A1AB=cos∠A1AO·cos∠OAB
∴ cos∠A1AO=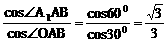
∴ sin∠A1AO=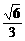
∴ A1O=A1Asin∠A1AO=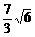
∴ 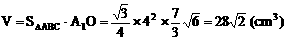
(4)把线A1A到侧面BB1C1C的距离转化为点A或A1到平面BB1C1C的距离
为了找到A1在侧面BB1C1C上的射影,首先要找到侧面BB1C1C的垂面
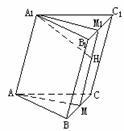 设平面AA1M交侧面BB1C1C于MM1
设平面AA1M交侧面BB1C1C于MM1
∵ BC⊥AM,BC⊥A1A
∴ BC⊥平面AA1M1M
∴ 平面AA1M1M⊥侧面BCC1B1
在平行四边形AA1M1M中
过A1作A1H⊥M1M,H为垂足
则A1H⊥侧面BB1C1C
∴ 线段A1H长度就是A1A到侧面BB1C1C的距离
∴ 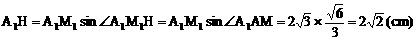
例4、平面α内有半径为R的⊙O,过直径AB的端点A作PA⊥α,PA=a,C是⊙O上一点,∠CAB=600,求三棱锥P-OBC的侧面积。
解题思路分析:
三棱锥P-OBC的侧面由△POB、△POC、△PBC三个三角形组成
在求出边长元素后,求三角形面积时,应注意分析三角形的形状,简化计算
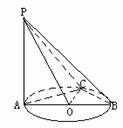 ∵ PA⊥平面ABC
∵ PA⊥平面ABC
∴ PA⊥AO,AC为PC在平面ABC上的射影
∵ BC⊥AC
∴ BC⊥PC
△ POB中,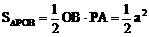
△ PBC中,BC=ABsin600=2a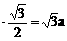
∴ AC=a
∴ PC=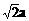
∴ 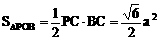
△ POC中,PO=PC=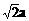 ,OC=a
,OC=a
∴ 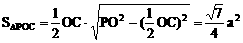
∴ S侧=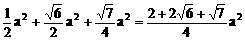
例5、四棱锥V-ABCD底面是边长为4的菱形,∠BAD=1200,VA⊥底面ABCD,VA=3,AC与BD交于O,(1)求点V到CD的距离;(2)求点V到BD的距离;(3)作OF⊥VC,垂足为F,证明OF是BD与VC的公垂线段;(4)求异面直线BD与VC间的距离。
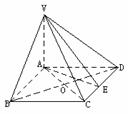 解题思路分析:
解题思路分析:
(1) 用三垂线定理作点到线的垂线
在平面ABCD内作AE⊥CD,E为垂足
∵ VA⊥平面ABCD
∴ AE为VE在平面ABCD上的射影
∴ VE⊥CD
∴ 线段VE长为点V到直线CD的距离
∵ ∠BAD=1200
∴ ∠ADC=600
∴ △ACD为正三角形
∴ E为CD中点,AE=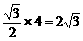
∴ VE=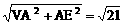
(2)∵ AO⊥BD
∴ 由三垂线定理VO⊥BD
∴ VO长度为V到直线BD距离
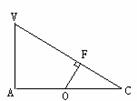 VO=
VO=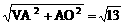
(3)只需证OF⊥BD
∵ BD⊥HC,BD⊥VA
∴ BD⊥平面VAC
∴ BD⊥OF
∴ OF为异面直线BD与VC的公垂线
(4)求出OF长度即可
在Rt△VAC中
OC=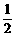 AC=2,VC=
AC=2,VC=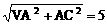
∴
OF=OC·sin∠ACF=OC·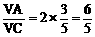
(三)解答题
11、在棱长为1的正方体ABCD-A1B1C1D1中,E、F分别是D1D,DB的中点,G在棱CD上,CG=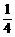 CD,H是C1G的中点
CD,H是C1G的中点
(1) 求证:EF⊥B1C
(2) 求EF与C1G所成角的余弦值
(3) 求FH的长
12、长方体ABCD-A1B1C1D1中,AB=a,BC=b,AA1=c,(a>b),求异面直线D1B和AC所成角的余弦值。
13、M、N分别是正方体ABCD-A1B1C1D1的棱BB1和B1C1的中点,
(1) 求MN与CD所成的角;
(2) 求MN与AD所成的角。
14、长方体ABCD-A1B1C1D1中,AB=2AA1=2BC,E为C1D1中点,求证:DE⊥平面EBC。
15、正方体ABCD-A1B1C1D1中,E为CD的中点
(1) 求证:EB1⊥AD1;
(2) 求D1E与A1C所成角的余弦值。
第7讲棱柱和棱锥
(二) 填空题
6、已知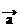 =(3,-3,-1),
=(3,-3,-1),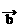 =(2,0,3),
=(2,0,3),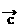 =(0,0,2),求
=(0,0,2),求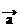 ·(
·(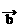 +
+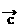 )=__________。
)=__________。
7、
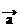 =(2,-3,
=(2,-3,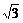 ),
),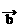 =(1,0,0),则
=(1,0,0),则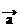 与
与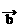 夹角为__________。
夹角为__________。
8、 与xoy平面的距离为1的点(x,y,z)所满足的条件是__________。
9、已知点A(3,-5,7),点B(1,-4,2),则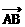 的坐标是__________,AB中点坐标是__________。
的坐标是__________,AB中点坐标是__________。
10、已知A(3,2,1),B(1,0,4),则到A、B两点距离相等的点(x,y,z)的坐标所满足的条件是__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com