
题目列表(包括答案和解析)
1、
设全集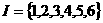 ,集合
,集合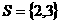 ,集合
,集合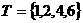 ,则
,则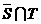 的真子集共有
的真子集共有
 个。
个。
2、 二次函数、二次不等式、二次方程的关系。
[例题]
例1、如果函数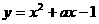 在区间
在区间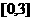 上有最小值
上有最小值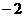 ,那么实数
,那么实数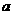 的值为()
的值为()
A、2 B、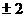 C、
C、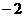 D、
D、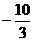
例2、已知二次函数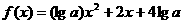 的最大值为3,求
的最大值为3,求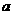 的值。
的值。
例3、 二次函数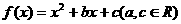 且
且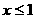 时,
时,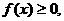 当
当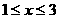 时,
时,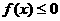 恒成立;
恒成立;
(1)求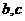 之间的关系;
之间的关系;
(2)当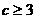 时,是否存在实数
时,是否存在实数 ,使得
,使得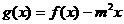 在区间
在区间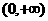 上是单调函数?若存在,求出
上是单调函数?若存在,求出 的范围,若不存在,说明理由。
的范围,若不存在,说明理由。
例4、设二次函数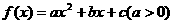 ,方程
,方程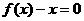 的两根为
的两根为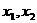 ,满足
,满足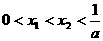 ;
;
(1)当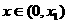 时,证明:
时,证明: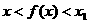
(2)设函数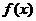 的图象关于直线
的图象关于直线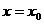 对称,证明:
对称,证明: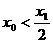 。
。
[练习]1、二次函数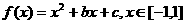
(I)用定义证明:当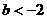 时,
时,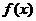 在
在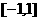 上是减函数;
上是减函数;
(II)当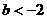 时,在
时,在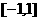 上是否存在一个
上是否存在一个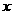 使得
使得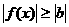 ;
;
(III)若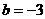 且
且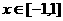 上,
上,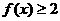 恒成立,求
恒成立,求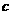 的取值范围。
的取值范围。
集合
[基本知识]
1、 二次函数的图象和性质;
20.当兔子和狐狸处于同一栖息地时,忽略其他因素,只考虑兔子数量和狐狸数量的相互影响,为了简便起见,不妨做如下假设:
(1)由于自然繁殖,兔子数每年增长10%,狐狸数每年减少15%;
(2)由于狐狸吃兔子,兔子数每年减少狐狸数的0.15倍,狐狸数每年增加兔子数的0.1倍;
(3)第n年时,兔子数量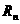 用表示,狐狸数量用
用表示,狐狸数量用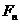 表示;
表示;
(4)初始时刻(即第0年),兔子数量有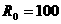 只,狐狸数量有
只,狐狸数量有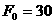 只。
只。
请用所学知识解决如下问题:
(1)列出兔子与狐狸的生态模型; (2)求出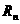 、
、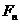 关于n的关系式;
关于n的关系式;
(3)讨论当n越来越大时,兔子与狐狸的数量是否能达到一个稳定的平衡状态,说明你的理由。
解:⑴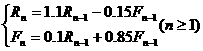 ……………………4’
……………………4’
⑵设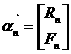 ,
,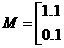
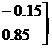
∴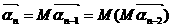 =……=
=……=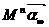
又矩阵M的特征多项式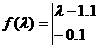
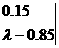
=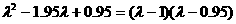
令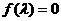 得:
得: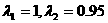
特征值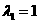 对应的一个特征向量为
对应的一个特征向量为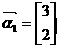
特征值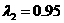 对应的一个特征向量为
对应的一个特征向量为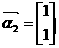 ……………………6’
……………………6’
且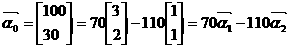
∴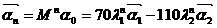 =
=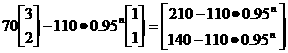
∴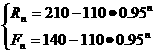 ………………………………14’
………………………………14’
⑶当n越来越大时,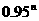 越来越接近于0,
越来越接近于0,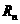 ,
,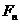 分别趋向于常量210,140。即随着时间的增加,兔子与狐狸的数量逐渐增加,当时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态。……2’
分别趋向于常量210,140。即随着时间的增加,兔子与狐狸的数量逐渐增加,当时间充分长后,兔子与狐狸的数量达到一个稳定的平衡状态。……2’
19.在一个盒子中,放有标号分别为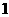 ,
,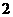 ,
,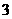 的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为
的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片的标号分别为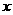 、
、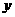 ,记
,记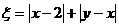 .
.
(Ⅰ)求随机变量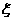 的最大值,并求事件“
的最大值,并求事件“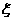 取得最大值”的概率;
取得最大值”的概率;
(Ⅱ)求随机变量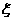 的分布列和数学期望.
的分布列和数学期望.
解:(Ⅰ)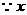 、
、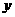 可能的取值为
可能的取值为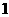 、
、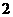 、
、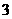 ,
,
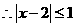 ,
,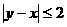 ,
, 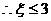 ,且当
,且当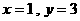 或
或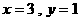 时,
时,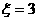
因此,随机变量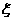 的最大值为
的最大值为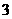 .
.  有放回抽两张卡片的所有情况有
有放回抽两张卡片的所有情况有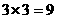 种,
种,
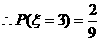 .
.
答:随机变量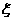 的最大值为3,事件“
的最大值为3,事件“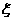 取得最大值”的概率为
取得最大值”的概率为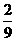 .
.
(Ⅱ)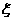 的所有取值为
的所有取值为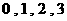 .
.
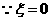 时,只有
时,只有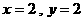 这一种情况,
这一种情况,
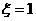 时,有
时,有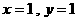 或
或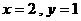 或
或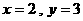 或
或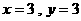 四种情况,
四种情况,
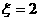 时,有
时,有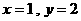 或
或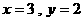 两种情况.
两种情况.
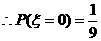 ,
,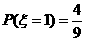 ,
,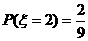 .
.
则随机变量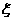 的分布列为:
的分布列为:
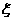

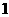
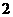
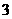
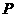
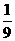
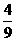
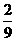
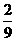
因此,数学期望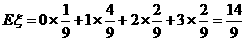 .
.
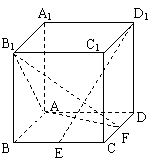
18.如图,正方体ABCD-A1B1C1D1中,点E是棱BC的中点,点F 是棱CD上的动点.
(Ⅰ)试确定点F的位置,使得D1E⊥平面AB1F;
(Ⅱ)当D1E⊥平面AB1F时,求二面角C1―EF―A的余弦值以及BA1与面C1EF所成的角的大小.
解:(1)以A为原点,直线AB、AD、AA1为x轴、y轴、z轴建立空间直角坐标系,
不妨设正方体的棱长为1,且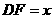 ,则
,则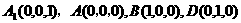
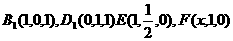
于是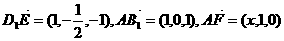
由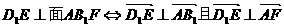
于是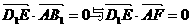 ,可解得
,可解得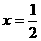
所以当点F是CD的中点时,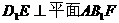
(2)当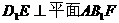 时,F是CD的中点,
时,F是CD的中点,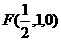
平面AEF的一个法向量为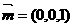
而在平面C1EF中,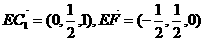
所以平面C1EF的一个法向量为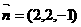
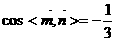 ,
,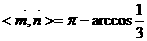
又因为当把 ,
,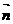 都移向这个二面角内一点时,
都移向这个二面角内一点时, 背向平面AEF,而
背向平面AEF,而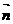 指向平面C1EF
指向平面C1EF
故二面角C1―EF―A的大小为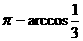
又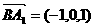 ,
, 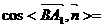
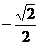 , 所以
, 所以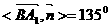
 BA1与平面C1EF所成的角的大小为
BA1与平面C1EF所成的角的大小为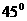 .
.
17.设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内.
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
解:(1)C52A54=1200(种) ……4分
(2)A55-1=119(种) ……8分
(3)满足的情形:第一类,五个球的编号与盒子编号全同的放法:1种
第二类,四个球的编号与盒子编号相同的放法:0种
第三类,三个球的编号与盒子编号相同的放法:10种
第四类,二个球的编号与盒子编号相同的放法:2C52=20种
∴ 满足条件的放法数为:
1+10+20=31(种) ……14分
16.函数数列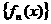 满足:
满足: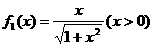 ,
,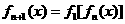
(1)求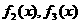 ;
;
(2)猜想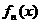 的表达式,并证明你的结论。
的表达式,并证明你的结论。
解:⑴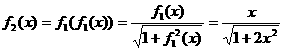 …………2’
…………2’
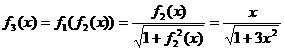 …………2’
…………2’
⑵猜想: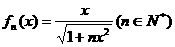 ……………………3’
……………………3’
下面用数学归纳法证明:
①当n=1时,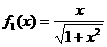 ,已知,显然成立………………1’
,已知,显然成立………………1’
②假设当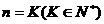 时 ,猜想成立,即
时 ,猜想成立,即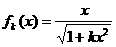
则当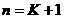 时,
时,
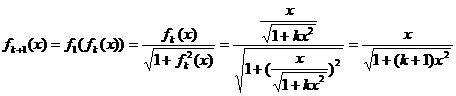 ……3’
……3’
即对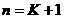 时,猜想也成立。
时,猜想也成立。
结合①②可知:猜想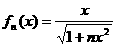 对一切
对一切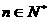 都成立。………………2’
都成立。………………2’
15.设虚数z1,z2,满足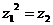 .
.
(1)若z1,z2又是一个实系数一元二次方程的两根,求z1, z2.
(2)若z1=1+mi(i为虚数单位,m∈R), 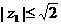 ,复数w=z2+3,求|w|的取值范围.
,复数w=z2+3,求|w|的取值范围.
解:(1)∵z1, z2是一个实系数一元二次方程的两个虚根,因此必共轭,
可设z1=a+bi(a,b∈R且b≠0),则z2=a-bi,
由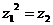 得(a+bi)2=a-bi 即:
a2-b2+2abi=a-bi
得(a+bi)2=a-bi 即:
a2-b2+2abi=a-bi
根据复数相等,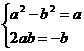 ∵b≠0 解得:
∵b≠0 解得: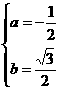 或
或 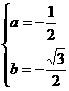 ,
,
∴ 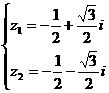 或
或 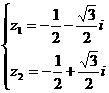 .
.
(2)由于 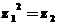 ,z1=1+mi, w=z2+3, ∴w=(1+mi)2+3=4-m2+2mi.
,z1=1+mi, w=z2+3, ∴w=(1+mi)2+3=4-m2+2mi.
∴  ,
,
由于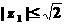 且m≠0, 可解得0<m2≤1, 令m2=u,
且m≠0, 可解得0<m2≤1, 令m2=u, 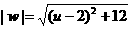 ,
,
在u∈(0,1)上,(u-2)2+12是减函数,∴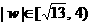 .
.
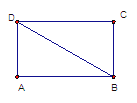
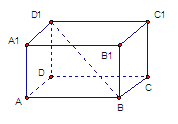
14.如图,已知命题:若矩形ABCD的对角线BD与边AB和BC所成角分别为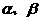 ,则
,则 若把它推广到长方体ABCD-A1B1C1D1中,试写出相应命题形式:
若把它推广到长方体ABCD-A1B1C1D1中,试写出相应命题形式:
若长方体ABCD-A1B1C1D1的对角线BD1与BA1,BB1,BC所成的角分别为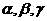 ,则
,则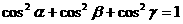 。.
。.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com