1.如图，设F是抛物线的焦点，M是抛物线上任意一点，MT是抛物线在M的切线，MN是法线，ME是平行于抛物线的轴的直线.求证：法线MN必平分∠FME，即φ₁=φ₂.

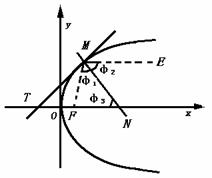
解：取坐标系如图，这时抛物线方程为y²=2px.(p＞0)，因为ME平行x轴(抛物线的轴)，∴φ₁=φ₂,只要证明φ₁=φ₃，也就是△FMN的两边FM和FN相等.设点M的坐标为(x₀,y₀)，则法线MN的方程是y-y₀=-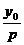(x-x₀),令y=0，便得到法线与x轴的交点N的坐标(x₀+p,0)，所以｜FN｜=｜x₀+p-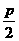｜=x₀+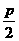,又由抛物线的定义可知，｜MF｜=x₀+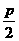,∴｜FN｜=｜FM｜,由此得到φ₁=φ₂=φ₃，若M与顶点O重合，则法线为x轴，结论仍然成立.

2.参与设计小花园的喷水池活动.

要求水流形状美观，水流不落池外.

[知识探究学习]

1.求函数y=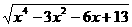-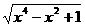的最大值.

解：将函数变形为y=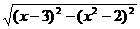-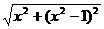，由几何意义知，y可以看成在抛物线f(x)=x²上的点P(x,x²)到两定点A(3，2)和B(0，1)的距离之差，∵｜PA｜-｜PB｜≤｜AB｜，∴当P、A、B三点共线，且P在B的左方时取等号，此时P点为AB与抛物线的交点，即P为(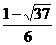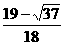，)时，y_max=｜AB｜=.

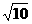2.公园要建造一个圆形的喷水池，在水池中央垂直于水面安装一个柱子OA，O恰在圆形水面中心，OA=1.25米.安置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路经落下，且在过OA的任一平面上抛物线路径如图所示，为使水流形状较为漂亮，设计成水流在到OA距离1米处达到距水面最大高度2.25米.如果不计其它因素，那么水池的半径至少要多少米，才能使喷出的水流不致落到池外?

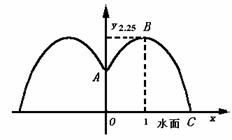
分析　 根据图形的对称性，设出并求出一边的抛物线的方程，便可求出水池的半径.

以OA所在直线为y轴，过O点作oy轴的垂直线ox轴，建立直角坐标系如图

依题意A(0，1.25)，设右侧抛物线顶点为则B(1，2.25)，抛物线与x轴正向交点为C，OC即圆型水池的半径.

设抛物线ABC的方程为

(x-1)²=-2p(y-2.25)

将A(0，1.25)代入求得p=

∴抛物线方程为(x-1)²=-(y-2.25)

令y=0，(x-1)²=1.5²,x=2.5(米)

即水池的半径至少要2.5米，才能使喷出的水流不致落到池外.

[知识验证实验]

1.已知点P(x₀,y₀)在抛物线含焦点的区域内，求证以点P为中点的抛物线y²=2px(p＞0)的中点弦方程为

yy₀-p(x+x₀)=y²₀-2px₀

注：运用求中点弦的方法不难求出结论，这一结论和过抛物线y²=2px上点的切线方程有什么联系?

若P(x₀,y₀)为非对称中心，将抛物线y²=2px换成椭圆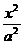+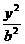=1或双曲线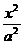-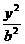=1，它们的中点弦存在的话，中点弦方程又将如何?证明你的结论.

中点弦方程在高考中多以选择题、填空题的形式出现.

10.已知抛物线y²=4ax(0＜a＜1)的焦点为F，以A(a+4,0)为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点，

(Ⅰ)求｜MF｜+｜NF｜的值；

(Ⅱ)是否存在这样的a值，使｜MF｜、｜PF｜、｜NF｜成等差数列?如存在，求出a的值，若不存在，说明理由.

[生活实际运用]

9.已知圆C过定点A(0，p)(p＞0)，圆心C在抛物线x²=2py上运动，若MN为圆C在x轴上截得的弦，设｜AM｜=m,｜AN｜=n，∠MAN=θ.(1)当点C运动时，｜MN｜是否变化?写出并证明你的结论?(2)求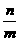+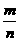的最大值，并求取得最大值时θ的值和此时圆C的方程.

8.已知过抛物线y²=2px的焦点F的弦AB被F分成长度为m、n的两部分，则+=　　 　　　　　　.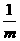

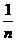7.已知抛物线y²=2x的弦过定点(-2，0)，则弦AB中点的轨迹方程是　　　　　　　 .