
题目列表(包括答案和解析)
5.函数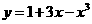 有
( )
有
( )
A.极小值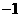 ,极大值
,极大值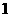 B.极小值
B.极小值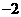 ,极大值
,极大值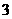
C.极小值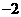 ,极大值
,极大值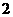 D.极小值
D.极小值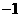 ,极大值
,极大值
4.三位文科班的学生挑战数学奥赛班学生小明,小明出一道竞赛题由三人解答,三人可解出的概率依次为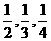 ,则三人独立解答仅有一人解出的概率为
( )
,则三人独立解答仅有一人解出的概率为
( )
A. 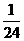 B.
B.
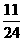 C.
C.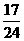 D.
D.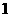
3.以一个正方体的顶点为顶点的四面体共有 ( )
A.70个 B.64个 C.58个 D.52个
2.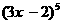 的展开式中
的展开式中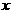 的系数是
( )
的系数是
( )
A.160 B.240 C.360 D.800
1.一个容量为32的样本,已知某组样本的频率为0.125,则该组样本的频数为 ( )A.2 B.4 C.6 D.8
25. (本题满分12分)
已知椭圆C: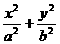 =1(
=1(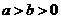 )的离心率为
)的离心率为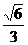 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为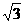 .
.
(Ⅰ)求椭圆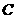 的方程;
的方程;
(Ⅱ)设直线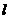 与椭圆
与椭圆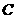 交于
交于 、
、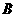 两点,坐标原点
两点,坐标原点 到直线
到直线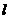 的距离为
的距离为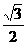 ,求△
,求△ 面积的最大值。
面积的最大值。
解:(Ⅰ)设椭圆的半焦距为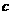 ,依题意
,依题意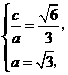 ∴
∴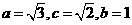
∴ 所求椭圆方程为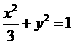 .
---------------------4分
.
---------------------4分
(Ⅱ)设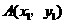 ,
,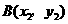 .
.
(1)当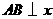 轴时,
轴时,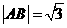 ,
,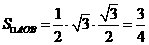 ---------------------5分
---------------------5分
(2)当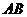 与
与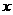 轴不垂直时,设直线
轴不垂直时,设直线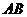 的方程为
的方程为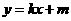 .
.
由已知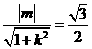 ,得
,得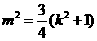 .
.
把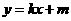 代入椭圆方程,整理得
代入椭圆方程,整理得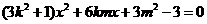 ,
,
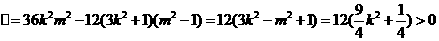
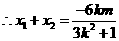 ,
,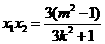 .
----------------------7分
.
----------------------7分
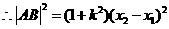
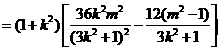
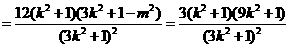
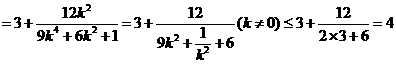 .--------------10分
.--------------10分
当且仅当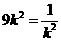 ,即
,即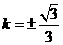 时等号成立,
时等号成立, 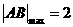 .
.
当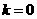 时,
时,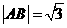 ,
,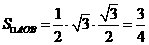
综上所述当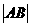 最大时,
最大时, 面积取最大值
面积取最大值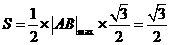 .------12分
.------12分
本资料由《七彩教育网》 提供!
24. (本题满分10分)
已知函数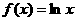 ,
,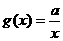 ,设
,设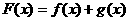 .
.
(Ⅰ)当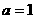 时,求函数
时,求函数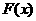 的单调区间;
的单调区间;
(Ⅱ)若以函数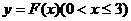 图象上任意一点
图象上任意一点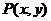 为切点的切线斜率
为切点的切线斜率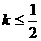 恒成立,
恒成立,
求实数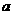 的取值范围。
的取值范围。
解: (Ⅰ)由已知可得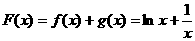 ,函数的定义域为
,函数的定义域为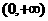 -----------------1分
-----------------1分
则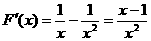 ,由
,由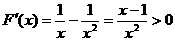
可得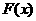 在区间
在区间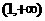 上单调递增,
-----------------------3分
上单调递增,
-----------------------3分
由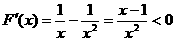 得
得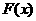 在
在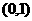 上单调递减。 ------------------------5分
上单调递减。 ------------------------5分
(Ⅱ)由题意可知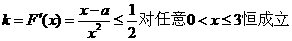 ,
,
即有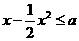
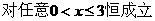 ,即
,即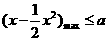 -------------------8分
-------------------8分
令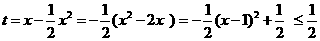
则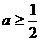 ,即实数
,即实数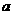 的取值范围
的取值范围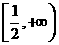 ----------------------10分
----------------------10分
17、(本题满分12分)
某市旅游部门开发一种旅游纪念品,每件产品的成本是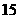 元,销售价是
元,销售价是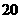 元,月平均销售
元,月平均销售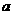 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为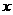
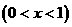 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为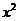 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是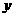 (元).
(元).
(Ⅰ)写出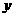 与
与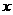 的函数关系式;
的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大。
解:(Ⅰ)设改进工艺后,每件产品的销售价为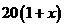 元,月平均销售量为
元,月平均销售量为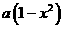 件,
件,
则月平均利润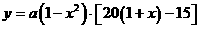 (元),
--------5分
(元),
--------5分
∴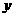 与
与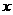 的函数关系式为
的函数关系式为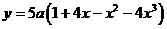
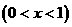 …………6分
…………6分
(Ⅱ)由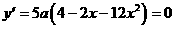 得
得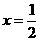 或
或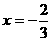 (舍), ……………8分
(舍), ……………8分
当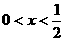 时
时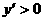 ;
;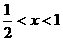 时
时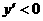 ,
故
,
故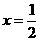 是函数y的极大值点,
是函数y的极大值点,
也是最大值点,∴函数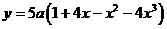
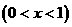 在
在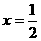 取得最大值.---11分
取得最大值.---11分
故改进工艺后,每件产品的销售价为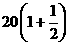
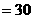 元时,旅游部门销售该纪念品的
元时,旅游部门销售该纪念品的
月平均利润最大. ……………………12分
16、(本题满分12分).
设动点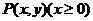 到定点
到定点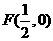 的距离比它到
的距离比它到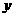 轴的距离大
轴的距离大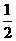 ,记点
,记点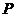 的轨迹为曲线
的轨迹为曲线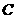
(Ⅰ)求点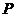 的轨迹方程;
的轨迹方程;
(Ⅱ)设圆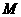 过
过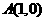 ,且圆心
,且圆心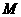 在点
在点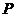 的轨迹上,
的轨迹上,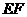 是圆
是圆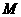 在
在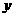 轴上截得的弦,请证明:
轴上截得的弦,请证明:
当圆心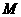 运动时,弦长
运动时,弦长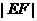 为定值,并求出此定值。
为定值,并求出此定值。
解:(Ⅰ)依题意,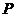 到
到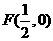 距离等于
距离等于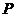 到直线
到直线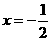 的距离,曲线
的距离,曲线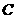 是以原点为顶点,
是以原点为顶点,
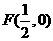 为焦点的抛物线 ---------------------2分
为焦点的抛物线 ---------------------2分
曲线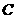 方程是
方程是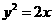 ----------------------4分
----------------------4分
(Ⅱ)设圆心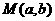 ,因为圆
,因为圆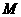 过
过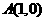
故设圆的方程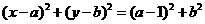 -----------------------6分
-----------------------6分
令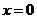 得:
得: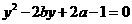
设圆与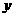 轴的两交点为
轴的两交点为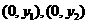 ,则
,则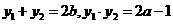 ------10分
------10分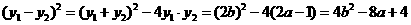
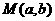 在抛物线
在抛物线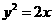 上,
上,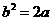 ,
, 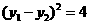 ,
,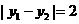
所以,当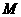 运动时,弦长
运动时,弦长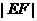 为定值2。 ----------------12分
为定值2。 ----------------12分
15、(本题满分10分)
已知函数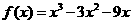 .
.
(Ⅰ)求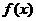 的单调递增区间; (Ⅱ)求
的单调递增区间; (Ⅱ)求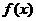 在区间
在区间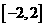 上的最值。
上的最值。
解:(Ⅰ)令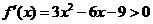 ,解得
,解得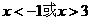 , ---------------4分
, ---------------4分
所以函数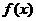 的单调递增区间为
的单调递增区间为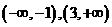 . ---------------5分
. ---------------5分
(Ⅱ) 当x变化时,f’(x)与f(x)的变化情况如下表:
|
x |
-2 |
(-2,-1) |
-1 |
(-1,2) |
2 |
|
f’(x) |
|
+ |
0 |
- |
|
|
f (x) |
-2 |
 |
极大值5 |
 |
-22 |
----------------8分
从而可知,当x=-1时,函数f(x)取得最大值5,即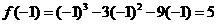 ,
,
当x=2时,函数f(x)取得最小值-22,即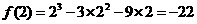 。-------10分
。-------10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com