
题目列表(包括答案和解析)
4、将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( )
A.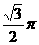 B.
B.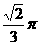 C.
C.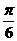 D.
D.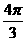
3、学校邀请6位同学的父母共12人,请这12位家长中的4位介绍对子女的教育经验,如果4位中恰有一对是夫妻,则不同的选择方法种数是( )
A.60 B.120 C.240 D.270
2、在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成角的正弦值为( )
A.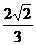 B.
B.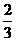 C.
C.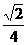 D.
D.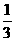
1、设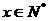 ,求
,求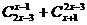 的值是( )
的值是( )
A.2或3或4 B.4或7或11 C.只有3 D.只有7
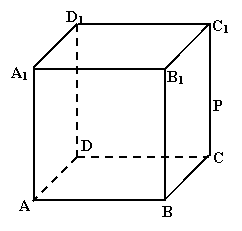
22.如图,在棱长为1的正方体ABCD-A1B1C1D1中,
P是侧棱CC1上的一点,CP=m。
(1) 试确定m使得直线AP与平面BDD1B1所成角
的正切值为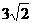 ;
;
(2) 在线段A1C1上是否存在一个定点Q,使得对任
意的m,D1Q在平面APD1上的射影垂直于AP。
并证明你的结论。
21. 某柑橘基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需要分两年实施;若实施方案一,预计第一年可以使柑橘产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑橘产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5。若实施方案二,预计第一年可以使柑橘产量恢复到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑橘产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6。实施每种方案,第二年与第一年相互独立。令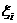 表示方案
表示方案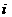 实施两年后柑橘产量达到灾前产量的倍数。
实施两年后柑橘产量达到灾前产量的倍数。
a)
写出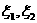 的分布列;
的分布列;
b) 实施哪种方案,两年后柑橘产量超过灾前产量的概率更大?
c) 不管哪种方案,如果实施两年后柑橘产量达不到、恰好达到、超过灾前产量,预计利润分别为10万元、15万元、20万元。问实施哪种方案的平均利润更大?
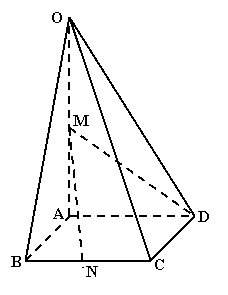
20.如图,在四棱锥O-ABCD中,底面ABCD是边长
为1的菱形,∠ABC=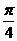 ,OA⊥底面ABCD,OA=2,
,OA⊥底面ABCD,OA=2,
M为OA的中点,N为BC的中点。
(1) 证明:直线MN∥平面OCD;
(2) 求异面直线AB与MD所成角的大小;
(3) 求点B到平面OCD的距离。
19.已知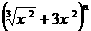 展开式各项系数的和比它的二项式系数的和大992。
展开式各项系数的和比它的二项式系数的和大992。
(1) 求n;
(2) 求展开式中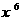 的项;
的项;
(3) 求展开式系数最大项。
18. . 甲乙等五名大冬会志愿者被随机的分到A,B,C,D四个不同的岗位服务,每岗位至少有一名志愿者。
(1) 求甲乙两人同时参加A岗位服务的概率;
(2) 求甲乙两人不在同一岗位服务的概率;
(3)
设随机变量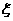 为这五名志愿者中参加A岗位服务的人数,求
为这五名志愿者中参加A岗位服务的人数,求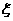 的分布列。
的分布列。
17. 从1,2,…,10这10个数字中有放回的抽取三次,每次抽取一个数字。
(1)取出的三个数字全不同的概率;
(2)三次抽取中最小数为3的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com