
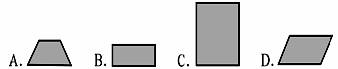
2.小华拿着一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影不可能是
1.-32的值是
A.6 B.-6 C.9 D.-9
26.(本题满分10分)
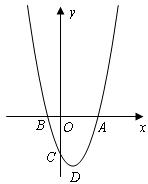
如下图,已知抛物线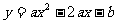 (
( )与
)与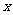 轴的一个交点为
轴的一个交点为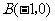 ,与y轴的负半轴交于点C,顶点为D.
,与y轴的负半轴交于点C,顶点为D.
(1)直接写出抛物线的对称轴,及抛物线与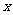 轴的另一个交点A的坐标;
轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点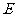 在抛物线的对称轴上,点
在抛物线的对称轴上,点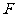 在抛物线上,且以
在抛物线上,且以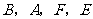 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点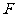 的坐标.
的坐标.
25.(本题满分10分)
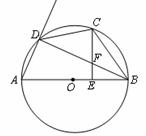
如下图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.
(1)求证: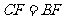 ;
;
(2)若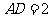 ,⊙O的半径为3,求BC的长.
,⊙O的半径为3,求BC的长.
24.(本题满分8分)
某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得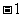 分。
分。
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
23.(本题满分8分)
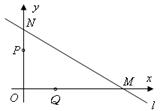
如下图,直线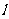 与
与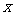 轴、
轴、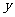 轴分别交于点
轴分别交于点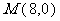 ,点
,点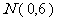 .点
.点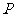 从点
从点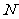 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿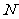 →
→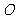 方向运动,点
方向运动,点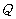 从点
从点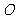 出发,以每秒2个单位长度的速度沿
出发,以每秒2个单位长度的速度沿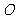 →
→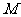 的方向运动.已知点
的方向运动.已知点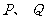 同时出发,当点
同时出发,当点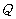 到达点
到达点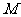 时,
时,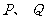 两点同时停止运动,设运动时间为
两点同时停止运动,设运动时间为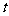 秒.
秒.
(1)设四边形MNPQ的面积为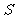 ,求
,求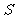 关于
关于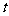 的函数关系式,并写出
的函数关系式,并写出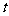 的取值范围.
的取值范围.
(2)当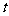 为何值时,
为何值时,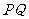 与
与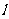 平行?
平行?
22.(本题满分6分)
如下图,热气球的探测器显示,从热气球看一栋高楼顶部的仰角为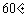 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为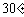 ,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:
,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据: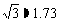 )
)
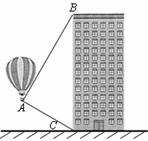
21.(本题满分6分)
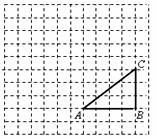
如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到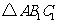 .
.
(1)在正方形网格中,作出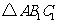 ;(不要求写作法)
;(不要求写作法)
(2)设网格小正方形的边长为1cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留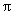 )
)
20.(本题满分6分)
如下图,四边形ABCD中,AB∥CD,∠B=∠D,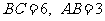 ,求四边形ABCD的周长.
,求四边形ABCD的周长.

19.(本题满分6分)
某学习小组对所在城区初中学生的视力情况进行抽样调查,图1是这些同学根据调查结果画出的条形统计图.请根据图中信息解决下列问题:
(1)本次抽查活动中共抽查了多少名学生?
(2)请估算该城区视力不低于4.8的学生所占的比例,用扇形统计图在图2中表示出来.
(3)假设该城区八年级共有4000名学生,请估计这些学生中视力低于4.8的学生约有多少人?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com