
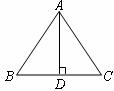
6.如图,等腰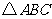 中,
中,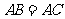 ,
,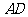 是底边上的高,若
是底边上的高,若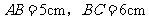 ,则
,则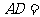 cm.
cm.
5.如图,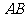 是
是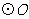 的直径,
的直径,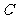 是
是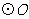 上一点,
上一点,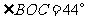 ,则
,则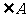 的度数为 .
的度数为 .
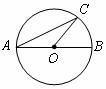
4.如图,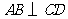 于点
于点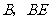 是
是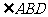 的平分线,则
的平分线,则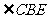 的度数为 .
的度数为 .
3.据报道,今年“五·一”期间我市旅游总收入同比增长超过两成,达到563 000 000元,用科学记数法表示为 元.
2.因式分解: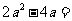 .
.
1.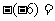 .
.
26.(本小题满分13分)
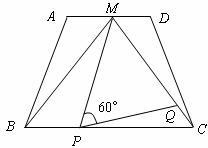
如下图,在梯形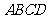 中,
中,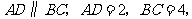 点
点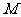 是
是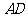 的中点,
的中点,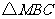 是等边三角形.
是等边三角形.
(1)求证:梯形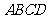 是等腰梯形;
是等腰梯形;
(2)动点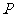 、
、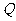 分别在线段
分别在线段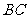 和
和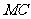 上运动,且
上运动,且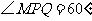 保持不变.设
保持不变.设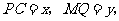 求
求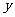 与
与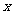 的函数关系式;
的函数关系式;
(3)在(2)中:①当动点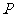 、
、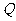 运动到何处时,以点
运动到何处时,以点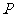 、
、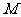 和点
和点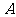 、
、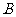 、
、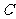 、
、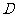 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;
②当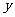 取最小值时,判断
取最小值时,判断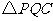 的形状,并说明理由.
的形状,并说明理由.
25.(本小题满分10分)
为实现区域教育均衡发展,我市计划对某县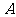 、
、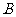 两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所
两类薄弱学校全部进行改造.根据预算,共需资金1575万元.改造一所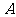 类学校和两所
类学校和两所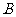 类学校共需资金230万元;改造两所
类学校共需资金230万元;改造两所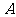 类学校和一所
类学校和一所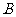 类学校共需资金205万元.
类学校共需资金205万元.
(1)改造一所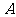 类学校和一所
类学校和一所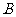 类学校所需的资金分别是多少万元?
类学校所需的资金分别是多少万元?
(2)若该县的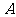 类学校不超过5所,则
类学校不超过5所,则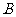 类学校至少有多少所?
类学校至少有多少所?
(3)我市计划今年对该县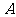 、
、 两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到
两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担.若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到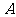 、
、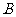 两类学校的改造资金分别为每所10万元和15万元。请你通过计算求出有几种改造方案?
两类学校的改造资金分别为每所10万元和15万元。请你通过计算求出有几种改造方案?
24.(本小题满分10分)
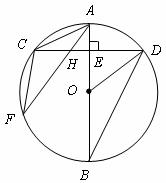
如下图,已知:在⊙O中,直径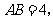 点
点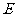 是
是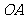 上任意一点,过
上任意一点,过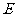 作弦
作弦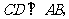 点
点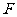 是
是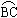 上一点,连接
上一点,连接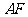 交
交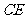 于
于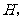 连接AC、CF、BD、OD.
连接AC、CF、BD、OD.
(1)求证: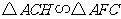 ;
;
(2)猜想: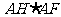 与
与 的数量关系,并说明你的猜想;
的数量关系,并说明你的猜想;
(3)探究:当点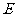 位于何处时,
位于何处时,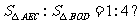 并加以说明.
并加以说明.
23.(本小题满分8分)
如下图所示,在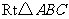 中,
中,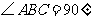 将
将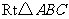 绕点
绕点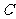 顺时针方向旋转
顺时针方向旋转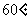 得到
得到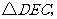 点
点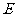 在
在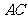 上,再将
上,再将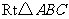 沿着
沿着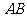 所在直线翻转
所在直线翻转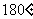 得到
得到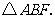 连接
连接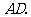
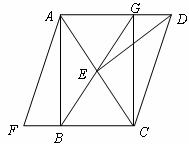
(1)求证:四边形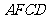 是菱形;
是菱形;
(2)连接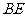 并延长交
并延长交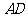 于
于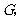 连接
连接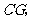 请问:四边形
请问:四边形 是什么特殊平行四边形?为什么?
是什么特殊平行四边形?为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com