
6.已知椭圆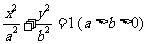 的左焦点为
的左焦点为 ,右顶点为
,右顶点为 ,点
,点 在椭圆上,且
在椭圆上,且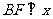 轴,直线
轴,直线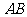 交
交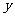 轴于点
轴于点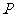 .若
.若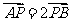 ,则椭圆的离心率是
,则椭圆的离心率是
A.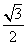 B.
B.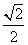 C.
C.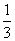 D.
D.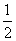
5.已知向量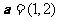 ,
,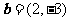 .若向量
.若向量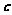 满足
满足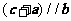 ,
,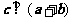 ,则
,则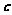
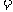
A.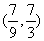 B.
B.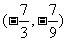 C.
C.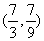 D.
D.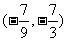
4.设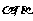 是两个不同的平面,
是两个不同的平面,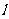 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是
A.若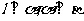 ,则
,则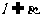 B.若
B.若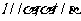 ,则
,则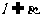
C.若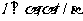 ,则
,则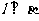 D.若
D.若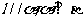 ,则
,则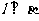
3.设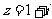 (
(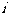 是虚数单位),则
是虚数单位),则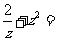
A. B.
B.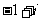 C.
C.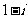 D.
D.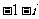
2.“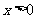 ”是“
”是“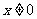 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.设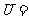
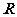 ,
,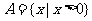 ,
,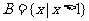 ,则
,则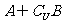 =
=
A.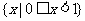 B.
B.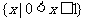 C.
C.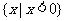 D.
D.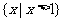
22.(本题满分14分)已知函数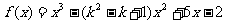 ,
,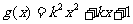 ,其中
,其中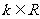 .
.
(Ⅰ)设函数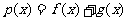 ,若
,若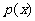 在区间(0,3)上不单调,求
在区间(0,3)上不单调,求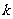 的取值范围;
的取值范围;
(Ⅱ)设函数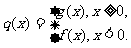 是否存在
是否存在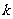 ,对任意给定的非零实数
,对任意给定的非零实数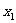 ,存在惟一的非零实数
,存在惟一的非零实数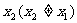 ,使得
,使得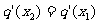 成立?若存在,求
成立?若存在,求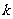 的值;如不存在,请说明理由.
的值;如不存在,请说明理由.
21.(本小题满分15分)已知椭圆C1: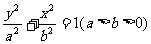 的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
的右顶点为A(1,0),过C1的焦点且垂直长轴的弦长为1.
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设点P的抛物线C2: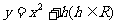 上,C2在点P处的切线与C1交于点M,N,当线段AP的中点与MN的中点的横坐标相等时,求
上,C2在点P处的切线与C1交于点M,N,当线段AP的中点与MN的中点的横坐标相等时,求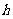 的最小值.
的最小值.
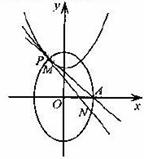
20.(本题满分15分)如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E、F、O分别为PA、PB、AC的中点,AC=16,PA=PC=10.
(Ⅰ)设G是OC的中点,证明FG//平面BOE;
(Ⅱ)证明:在△ABO内存在一点M,使FM⊥平面BOE,并求点M到OA,OB的距离.
19.(本题满分14分)在1,2,3,…,9这9个自然数中,任取3个数.
(Ⅰ)求这3个数中恰有1个是偶数的概率;
(Ⅱ)记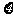 为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时
为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时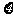 的值是2),求随机变量
的值是2),求随机变量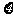 的分布列及其数学期望E
的分布列及其数学期望E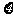 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com