
2.(文)设函数 .
.
(Ⅰ)求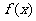 的最小值
的最小值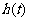 ;
;
(Ⅱ)若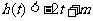 对
对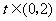 恒成立,求实数
恒成立,求实数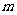 的取值范围.
的取值范围.
命题意图:
使文科学生熟悉导数的基本应用,巩固处理此类问题的通性通法.本题主要考查函数的单调性、极值以及函数导数的应用.
不等式
2.(理)已知函数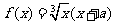 (
(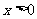 ,
,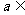 R)
R)
(1)求函数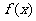 的单调区间;
的单调区间;
(2)求函数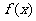 在
在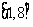 上的最大值和最小值.
上的最大值和最小值.
命题意图:
导数的应用,重点是单调性、极值、最值问题(或方程、不等式等可转化为最值的问题),要注意通性通法的落实.如果有参数,常常需要分类讨论:提取常数系数时,要注意系数是否可能为零;导数为零的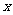 的值有多个时,要注意它们的大小关系是否是确定的等.
的值有多个时,要注意它们的大小关系是否是确定的等.
1.设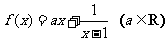 ,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.
,曲线y = f(x)在点(2,f(2))处的切线方程为y = x+3.
(1)求f(x)的解析式;
(2)若x∈[2,3]时,f(x)≥bx恒成立,求实数b的取值范围.
命题意图:
切线方程要注意“在点”和“过点”的区别;恒成立问题,存在性问题一般和最值、值域、单调性密切相关,当不等式两端都为变量时,一般要先分离变量.
2.已知点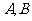 分别是直线
分别是直线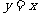 和
和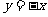 的动点(
的动点(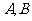 在
在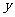 轴的同侧),且
轴的同侧),且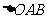 的面积为
的面积为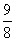 ,点
,点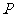 满足
满足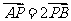 .
.
(1)试求点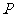 的轨迹
的轨迹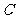 的方程;
的方程;
(2)已知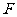
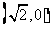 ,过
,过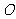 作直线
作直线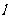 交轨迹
交轨迹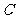 于两点
于两点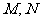 ,若
,若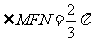 ,试求
,试求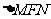 的面积.
的面积.
(3)理:已知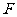
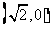 ,矩形
,矩形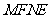 的两个顶点
的两个顶点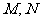 均在曲线
均在曲线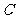 上,试求矩形
上,试求矩形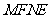 面积的最小值.
面积的最小值.
命题意图:
本题抓住解析几何重点研究问题设问,熟悉巩固通性通法,典型几何条件如长、角等的代数转换方法,让学生理解解析几何的基本思想与策略.解析几何要把握好条件的等价翻译,理顺各量间的关系,计算准确,进而得出正确结论.取值范围、最值、存在性、定值等问题是高中数学的重点题型,要重视。最值问题一般要建立函数关系(求哪个量的最值,这个量一般是因变量,关键是找到主动变化的量,即自变量),并且指出函数的定义域(定义域往往和判别式有关).解析几何考最值要注意均值定理、导数和二次函数的运用.
函数、导数
1.已知动点P到直线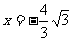 的距离是到定点(
的距离是到定点(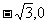 )的距离的
)的距离的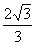 倍.
倍.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)如果直线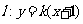
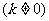 与P点的轨迹有两个交点A、B,求弦AB的垂直平分线在y轴上的截距
与P点的轨迹有两个交点A、B,求弦AB的垂直平分线在y轴上的截距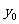 的取值范围.
的取值范围.
命题意图:
对解析几何两大基本问题:①求轨迹;②通过方程研究曲线性质进行再梳理.轨迹方程的求法一般分为直接法和间接法.直接法的步骤:建系设点,找等量关系,列方程,化简,检验;间接法的关键是找参数.如果明确说直线与圆锥曲线有两个不同的交点,一般是考查判别式与根系关系的应用.取值范围一般是函数的值域或不等式(组)的解集.
3.小明一家三口都会下棋。在假期里的每一天,父母都交替与小明下三盘棋,已知小明胜父亲的概率是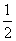 ,胜母亲的概率是
,胜母亲的概率是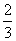 .
.
(1)如果小明与父亲先下,求小明恰胜一盘的概率;
(2)父母与小明约定,只要他在三盘中能至少连胜两盘,就给他奖品,那么小明为了获胜希望更大,他应该先与父亲下,还是先与母亲下?请用计算说明理由.
命题意图:
用数据说理和决策的意识.通过合理的分类、恰当的分步把复杂事件用相对简单(或已知概率)事件表示的能力,尤其是对(2)中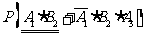
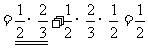 划线部分的理解;还要注意概率和不等式等其它数学知识的交汇.
划线部分的理解;还要注意概率和不等式等其它数学知识的交汇.
解析几何
2.文:某自助银行共有4台ATM机,在某一时刻A、B、C、D四台ATM机被占用的概率分别为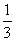 、
、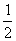 、
、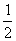 、
、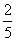 .
.
(Ⅰ)如果某客户只能使用A或B型号的ATM机,求该客户需要等待的概率;
(Ⅱ)求至多有三台ATM机被占用的概率;
(Ⅲ)求恰有两台ATM机被占用的概率.
命题意图:
概率主要考查两个公式(加法、乘法公式)、两个模型(古典概型、贝努里概型).
但要注意答题的规范性,不要只列一个算术式子来解答;注意两个公式适用的条件,互斥和独立;注意两个模型的辨别;对于“至多”,“至少”问题,常用对立事件计算.
1.理:某自助银行共有4台ATM机,在某一时刻A、B、C、D四台ATM机被占用的概率分别为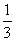 、
、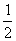 、
、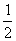 、
、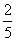 ,设某一时刻这家自助银行被占用的ATM机的台数为
,设某一时刻这家自助银行被占用的ATM机的台数为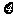
(Ⅰ)如果某客户只能使用A或B型号的ATM机,求该客户需要等待的概率;
(Ⅱ)求至多有三台ATM机被占用的概率;
(Ⅲ)求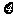 的分布列和数学期望.
的分布列和数学期望.
命题意图:
|
2.如图,二面角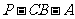 为直二面角,∠PCB=90°,
∠ACB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2,PM=1.
为直二面角,∠PCB=90°,
∠ACB=90°,PM∥BC,直线AM与直线PC所成的角为60°,又AC=1,BC=2,PM=1.
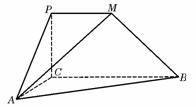
(Ⅰ)求证:AC⊥BM;
(Ⅱ)求二面角M-AB-C的正切值;
(III)求点P到平面ABM的距离.
命题意图:
用综合法解答立体几何问题,要注意步骤的规范性,如求二面角的大小,点到面的距离,要先证明,再计算。用向量方法解答,要注意两向量的夹角与所求角的关系,即相等、互补、互余等,还要注意所求角的范围,如斜线和平面所成角一定是锐角;要注意“体积法”在处理较难的角与距离问题中的灵活运用.
注意:立体几何重在通性、通法的熟练,逻辑的严谨,计算准确上.
概率
1.在直平行六面体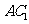 中,
中,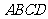 是菱形,
是菱形,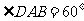 ,
,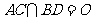 ,
,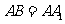 .
.
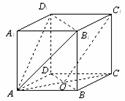
(1)求证: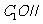 平面
平面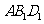 ;
;
(2)求证:平面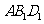
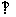 平面
平面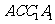 ;
;
(3)求直线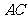 与平面
与平面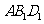 所成角的大小.
所成角的大小.
命题意图:
熟悉立体几何中常见问题及处理方法,要求学生敏锐把握所给图形特征,制定合理的解决问题策略.立体几何主要是两种位置关系(平行、垂直),两个度量性质(夹角、距离).解决问题的方法也有两种:几何方法和向量方法。两种方法各有优缺点,前者难在“找”和“作”的技巧性,后者难在建系和计算上,究竟用哪种方法,到时根据自己的情况决断.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com