
1.不等式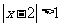 的解集是( )
的解集是( )
A.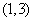 B.
B. C.
C. D.
D.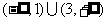
20.(本小题满分14分)
已知函数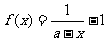 (其中a为常数,
(其中a为常数,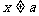 ),利用函数
),利用函数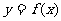
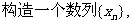 方法如下:对于给定的定义域中的x1,令
方法如下:对于给定的定义域中的x1,令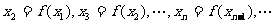
|
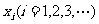 在定义域中,那么构造数列的过程继续下去;如果xi不在定义域中,那么构造数列的过程就停止。
在定义域中,那么构造数列的过程继续下去;如果xi不在定义域中,那么构造数列的过程就停止。
(1)当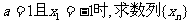 的通项公式;
的通项公式;
(2)如果可以用上述方法构造出一个常数列,求a的取值范围;
(3)是否存在实数a,使得取定义域中的任一实数值作为x1,都可用上述方法构造出一个无穷数列{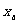 }?若存在,求出a的值;若不存在,请说明理由。
}?若存在,求出a的值;若不存在,请说明理由。
19.(本小题满分13分)
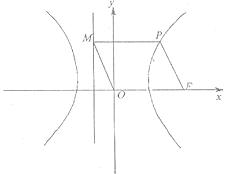
如图, F为双曲线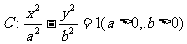 的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为菱形。
的右焦点,P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,O为坐标原点。已知四边形OFPM为菱形。
(1)求双曲线C的离心率;
(2)若经过焦点F且平行于OP的直线交双曲线于A、B两点,且|AB|=12,求此时双曲线方程。
18.(本小题满分13分)
在一次抗洪抢险中,准备用射击的方法引爆从河上游漂流而下的一只巨大汽油罐,已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中的概率都是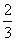 ,每次命中与否互相独立。
,每次命中与否互相独立。
(1)求恰好射击5次引爆油罐的概率;
(2)如果引爆或子弹打光则停止射击,设射击次数为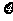 ,求
,求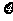 的分布列及
的分布列及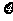 的数学期望.
的数学期望.
17.(本小题满分12分)
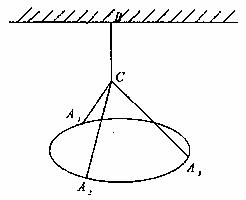
一个圆环直径为2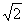 m,通过铁丝BC、CA1、CA2、CA3(A1、A2、A3是圆上三等分点)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
m,通过铁丝BC、CA1、CA2、CA3(A1、A2、A3是圆上三等分点)悬挂在B处,圆环呈水平状态并距天花板2m,如图所示。
(1)设BC长为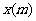 ,铁丝总长为
,铁丝总长为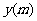 ,试写出y关于x的函数解析式,并写出函数定义域;
,试写出y关于x的函数解析式,并写出函数定义域;
(2)当x取多长时,铁丝总长y有最小值,并求此最小值。
16.(本小题满分14分)
如图,在三棱锥S-ABC中,底面ABC是边长为4的正三角形,侧面SAC⊥底面ABC,SA=SC=2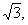 M、N分别为AB,SB的中点。
M、N分别为AB,SB的中点。
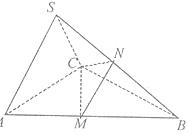
(1)求证:AC⊥SB;
(2)求二面角N-CM-B的大小。
15.(本小题满分13分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知向量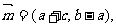
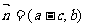 且
且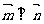 。
。
(1)求角C的大小;
(2)若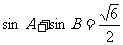 ,求角A的值。
,求角A的值。
14.在圆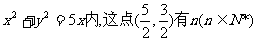 条弦,它们的长构成等比数列{
条弦,它们的长构成等比数列{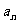 },若a1为过该点最短弦的长,an为过该点最长的弦的长,且公差
},若a1为过该点最短弦的长,an为过该点最长的弦的长,且公差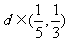 ,则n的值为
.
,则n的值为
.
13.6个人分乘两辆不同的出租车,如果每辆
|
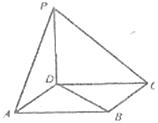
12.如图,PD⊥平面在ABCD,ABCD为正方形,PD=AD,则直线PA与直线BD所成的角为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com