
7.已知正数x、y满足等式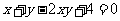 ,则( )
,则( )
A. xy的最大值是2,且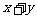 的最小值为4
的最小值为4
B. xy的最小值是4,且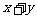 的最大值为4
的最大值为4
C. xy的最大值是2,且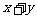 的最大值为4
的最大值为4
D. xy的最小值是4,且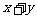 的最小值为4
的最小值为4
6.已知△ABC的三个顶点在同一球面上,∠BAC=900,AB=AC=2,若球心O到平面ABC的距离为1,则该球的表面积为( )
A. 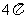 B.
B. 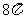 C.
C. 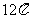 D.
D. 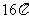
5.某一批袋装大米,质量服从正态分布N(10,0.01)(单位:kg),任选一袋大米,它的质量是9.8kg-10.2kg内的为(已知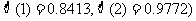
A. 0.8413 B. 0.9544 C. 0.9772 D. 0.6826
4.给出下列四个命题:
①若直线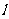 平面
平面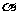 ,
,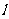 ∥平面
∥平面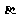 ,则
,则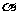 ⊥
⊥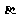 ;
;
②各侧面都是正方形的棱柱一定是正棱柱;
③一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面,则这两个二面角的平面角互为补角;
④过空间任意一点一定可以作一个和两条异面直线都平行的平面。
其中正确的命题的个数有(
)
A. 1 B. 2 C. 3 D.4
3.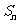 为等差数列
为等差数列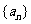 的前n项和,
的前n项和,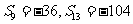 ,等比数列
,等比数列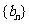 中,
中,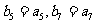 ,则
,则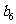 等于( )
等于( )
A. 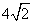 B.
B. 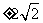 C.
C. 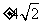 D. 32
D. 32
2.若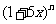 的展开式中各项系数之和为
的展开式中各项系数之和为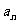 ,
,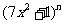 的展开式各项的二项式系数之和为
的展开式各项的二项式系数之和为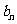 ,则
,则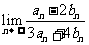 的值是( )
的值是( )
A. 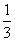 B.
B. 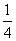 C.
1 D. -
C.
1 D. -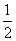
1.设集合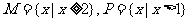 ,那么“
,那么“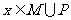 ”是“
”是“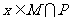 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
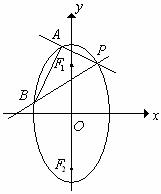
22.(本小题满分12分)已知椭圆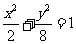 两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2、P是椭圆在第一象限弧上一点,并满足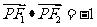 ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点
(1)求P点坐标;
(2)求证直线AB的斜率k为定值;
(3)求△PAB面积的最大值
21.(本小题满分12分)已知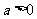 ,函数
,函数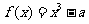 ,
,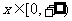 设
设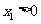 ,记曲线
,记曲线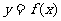 在点M(
在点M(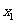 ,
,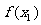 )处的切线为
)处的切线为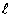
(1)求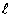 的方程;
的方程;
(2)设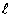 与x轴的交点为(x2,0),证明:①
与x轴的交点为(x2,0),证明:①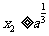 ;②若
;②若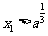 ,则
,则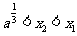
20.(本小题满分12分)如图所示,已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EAC∥D1B,且面EAC与底面ABCD所成的角为450,AB=a
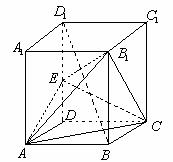
(1)求截面EAC的面积
(2)求异面直线A1B1与AC之间的距离;
(3)求三棱锥B1-EAC的体积

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com