
5.设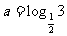 ,
,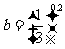 ,
,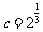 ,则( )
,则( )
A.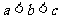 B.
B.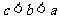 C.
C.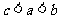 D.
D.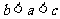
4.若函数f(x)=x3(x∈R),则函数y=f(-x )在其定义域上是( )
A.单调递减的偶函数 B.单调递减的奇函数
C.单凋递增的偶函数 D.单涮递增的奇函数
3.原点到直线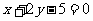 的距离为( )
的距离为( )
A.1 B.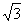 C.2 D.
C.2 D.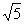
2.已知集合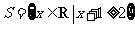 ,
, 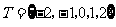 ,则
,则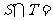 ( )
( )
A.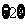 B.
B.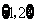 C.
C. D.
D.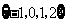
1.若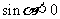 且
且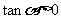 是,则
是,则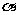 是( )
是( )
A.第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
22.(本小题满分14分)已知函数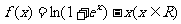 有下列性质:“若
有下列性质:“若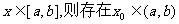 ,使得
,使得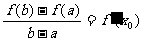 ”成立.
”成立.
(1)利用这个性质证明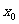 唯一;
唯一;
(2)设A、B、C是函数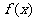 图象上三个不同的点,试判断△ABC的形状,并说明理由.
图象上三个不同的点,试判断△ABC的形状,并说明理由.
21.(本题满分12分)椭圆C的中心为坐标原点O,焦点在y轴上,离心率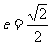 ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为 与y轴交于P点(0,m),与椭圆C交于相异两点A、B,且
与y轴交于P点(0,m),与椭圆C交于相异两点A、B,且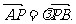
(1)求椭圆方程;
(2)若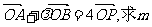 的取值范围.
的取值范围.
20.(本小题满分12分)已知数列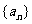 ,定义其倒均数是
,定义其倒均数是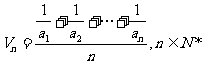 .
.
(1)求数列{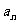 }的倒均数是
}的倒均数是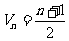 ,求数列{
,求数列{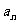 }的通项公式
}的通项公式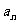 ;
;
(2)设等比数列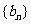 的首项为-1,公比为
的首项为-1,公比为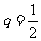 ,其倒数均为
,其倒数均为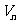 ,若存在正整数k,使得当
,若存在正整数k,使得当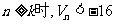 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
19.(本小题满分12分)某研究机构准备举行一次数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为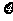 ,求随机变量
,求随机变量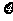 的变分布列和数学期望.
的变分布列和数学期望.
18.(本题满分12分)如下图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=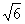 .
.
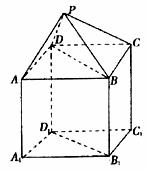
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成锐二面角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com