
8.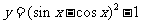 是 ( )
是 ( )
A.最小正周期为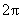 的偶函数 B.最小正周期为
的偶函数 B.最小正周期为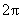 的奇函数
的奇函数
C.最小正周期为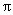 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为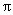 的奇函数
的奇函数
7.四个小动物换座位,开始是鼠、猴、兔、猫分别坐1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2009次互换座位后,小兔的座位对应的是 ( )
|
1 鼠 |
2 猴 |
|
1 兔 |
2 猫 |
|
1 猫 |
2 兔 |
|
1 猴 |
2 鼠 |
||||||
|
兔 3 |
猫 4 |
|
鼠 3 |
猴 4 |
|
猴 3 |
鼠 4 |
|
猫 3 |
兔 4 |
||||||
|
开始 |
|
第一次 |
|
第二次 |
|
第三次 |
||||||||||
A.编号1 B.编号2 C.编号3 D.编号4
6.函数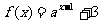 (a>0,且a≠1)的图像过一个定点P,且点P在直线
(a>0,且a≠1)的图像过一个定点P,且点P在直线
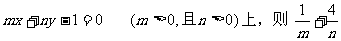 的最小值是 ( )
的最小值是 ( )
A.12 B.13 C.24 D.25
5.“a=1”是“函数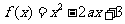 在区间[1,+∞)上为增函数”的( )条件
在区间[1,+∞)上为增函数”的( )条件
A.充分不必要 B.必要不充分
C.充要 D.不充分不必要
4.经过圆x2+2x+y2=0的圆心G,且与直线x+y=0垂直的直线方程是 ( )
A.x-y+1=0 B.x-y-1=0
C.x+y-1=0 D.x+y+1=0
3.已知平面向量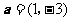 ,
,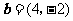 ,
,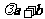 与
与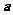 垂直,则
垂直,则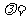 ( )
( )
A.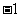 B.
B.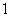 C.
C. D.
D.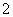
2.计算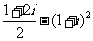 得 ( )
得 ( )
A.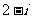 B.
B. C.
C.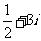 D.
D.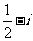
1.已知集合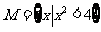 ,
,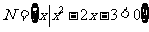 ,则集合
,则集合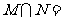 ( )
( )
A.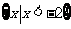 B.
B.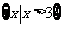
C.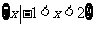 D.
D.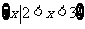
22.(本小题满分14分)
已知函数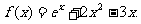
(I)求曲线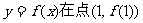 处的切线方程;
处的切线方程;
(Ⅱ)求证函数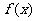 在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,
在区间[0,1]上存在唯一的极值点,并用二分法求函数取得极值时相应x的近似值(误差不超过0.2);(参考数据e≈2.7,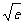 ≈1.6,e0.3≈1.3)
≈1.6,e0.3≈1.3)
(III)当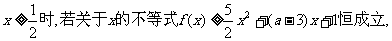 试求实数
试求实数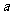 的取值范围。
的取值范围。
21.(本小题满分12分)
工厂生产某种产品,次品率p与日产量x(万件)间的关系为

已知每生产1件合格产品盈利3元,每出现重件次品亏损1.5元.
(I)将日盈利额y(万元)表示为日产量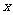 (万件)的函数;
(万件)的函数;
(Ⅱ)为使日盈利额最大,日产量应为多少万件?(注:次品率= ×100%)
×100%)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com