
22.(本小题满分14分)
设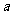 、
、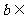 R,且
R,且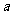 ≠2,
≠2,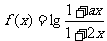 是定义在区间(-b,b)上的奇函数.
是定义在区间(-b,b)上的奇函数.
(Ⅰ)求实数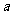 的值;
的值;
(Ⅱ)求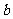 的取值范围.
的取值范围.
21.(本小题12分)
国家收购某种农产品价格为每吨120元,共中征税标准为每100元征收8元(称税率为8个百分点),计划可以收购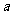 万吨,为减轻农民负担,决定税率降低
万吨,为减轻农民负担,决定税率降低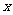 个百分点,预计收购量可增加
个百分点,预计收购量可增加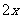 个百分点.如下表:
个百分点.如下表:
|
|
原计划 |
调整税率后 |
|
每吨价 |
120元 |
|
|
收购量 |
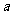 万吨 万吨 |
 |
|
征税标准 |
8% |
(8 )% )% |
(Ⅰ)写出降低税率后税收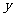 (万元)与
(万元)与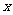 的函数关系式;
的函数关系式;
(Ⅱ)要使此项税收在税率调整后不低于原计划的78%,试确定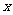 的范围.
的范围.
20.(本小题满分12分)
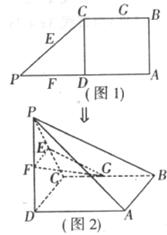
如图1,在直角梯形ABCP中,AP//BC,AP⊥AB,AB=BC=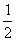 AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图2.
AP=2,D为AP的中点,E,F,G分别为PC、PD、CB的中点,将△PCD沿CD折起,使点P在平面ABCD内的射影为点D,如图2.
(Ⅰ)求证:AP//平面EFG;
(II)求三棱锥P-ABC的体积.
19.(本小题l2分)
求经过直线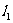 :
: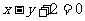 与直线
与直线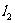 :
: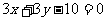 的交点,并且满足下列条件的直线的方程.
的交点,并且满足下列条件的直线的方程.
(Ⅰ)经过原点;
(Ⅱ)与直线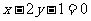 平行;
平行;
(Ⅲ)与直线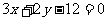 垂直.
垂直.
18.(本小题12分)
已知函数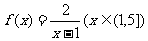 .
.
(Ⅰ)判断单调性并写出证明过程;
(Ⅱ)求函数的值域.
17.(本小题12分,每个6分.)
计算(Ⅰ)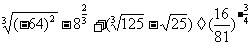 ;
;
(Ⅱ)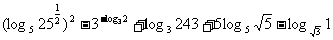 .
.
16.关于棱柱的特征叙述正确的是______________(把所有正确的序号都填上).
①两个底面是全等的多边形,且对应边互相平行;
②侧面是平行四边形;
③面数最少的棱柱是一个五面体;
④任何两条侧棱平行且相等;
⑤长方体是一个四棱柱,它的三视图是三个矩形;
⑥长方体ABCD-A1B1C1D1一定是由矩形ABCD平移得到的.
15.表面积为2的正方体的各个顶点都在球面上,则球的体积为___________.
14.与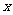 轴及点A(-4,2)的距离都是5的点的坐标是____________.
轴及点A(-4,2)的距离都是5的点的坐标是____________.
13.若对数函数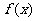 的图象过点(4,2),则
的图象过点(4,2),则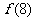 =____________.
=____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com