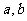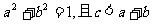4．若实数满足恒成立，则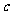的取值范围是　　　　 　　

A．　 　　　　　 B．　 　　　　　 C．　　 D．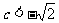

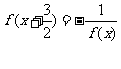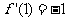3．若奇函数f(x)为满足，且，则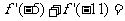　　　

A．1　　　 　　　　　　　 B．-1 　　　　　　　　　　 C．2　　　 　　　　 D．-2

2．等差数列的第2，3，6项顺次成等比数列，公差d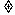0，则此等比数列的公比为　　　　

A．3　　　 　　　　　　　 B．4 　　　　　　　　　　　 C．5　　　 　　　　 D．15

1．设集合 , ,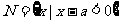若M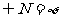,那么a的取值范围是　　

A．a<-2　　 　　　　　　　　 B．a-2 　　　　　　　　　 C．a-2　 　　　　 D．a-2 或 a4

22．(本小题满分14分)

　　　 设a∈R，函数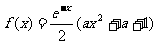，其中e是自然对数的底数。

　 (1)判断f(x)在R上的单调性；

　 (2)当-1＜a＜0，求f(x)在[1，2]上的最小值。

21．(本小题满分12分)

　　　 已知平面上一定点C(-1，0)和一定直线l：x=-4，P为该平面上一动点，作PQ⊥l，垂足为Q，且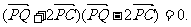

　 (1)求点P的轨迹方程；

　 (2)点O是坐标原点，过点C的直线与点P的轨迹交于A，B两点，求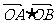的取值范围。

20．(本小题满分12分)

　　　 如图，直三棱柱ABC-A₁B₁C₁中，△ABC是等腰直角三角形，且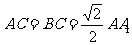，D为CC₁中点。

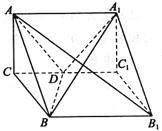
　 (1)求证AB₁⊥A₁BD；

　 (2)求二面角A-BD-A₁的大小。

19．(本小题满分12分)

　　　 已知等差数列{a_n}的前四项的和为60，第二项与第四项的和为34，等比数列{b_n}的前四项和为120，第二项与第四项的和为90.

　 (1)求数列{a_n}，{b_n}的通项公式；

　 (2)设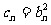，则数列{c_n}中的每一项是否都是数列{a_n}中的项，给出你的结论。并说明理由。

18．(本小题满分12分)

　　　 盒子中放了10个乒乓球，其中8个是新球，2个是旧球(即至少用过一次的球)。每次比赛，都拿出其中2个球用，用完后全部放回。

　 (1)设第一次比赛取出的两个球中新球的个数为，求随机变量的分布列和数学期望；

　 (2)求第二次比赛任取2球都是新球的概率。

17．(本小题满分12分)

　　　 已知函数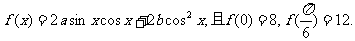

　 (1)求实数a，b的值

　 (2)求函数f(x)的最大值及取得最大值时x的值；