
4.
正项等比数列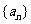 满足
满足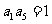 ,
,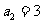 ,
,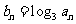 ,则数列
,则数列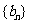 的前10项的和为
的前10项的和为
A.65 B.-65 C.25 D.-25
3. 设等差数列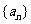 的公差为2,前n项的和为Sn,则下列结论中正确的是
的公差为2,前n项的和为Sn,则下列结论中正确的是
A.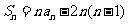 B.
B.
C.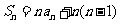 D.
D.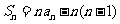
2. 集合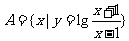 ,
,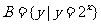 ,则
,则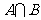 =
=
A.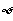 B.
B.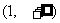 C.
C. D.
D.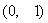
1.
a、b为实数,集合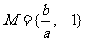 ,
,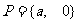 ,f :
,f : 表示把集合M中的元素x映射为集合P中仍为x,则a+b的值为
表示把集合M中的元素x映射为集合P中仍为x,则a+b的值为
A.-1 B.0 C.1 D.±1
22.(14分)已知函数f(x)=ax+b,当x∈[a1, b1]时,值域为[a2, b2]时,当x∈[a2, b2]时,值域为[a3, b3],…当x∈[an−1, bn−1]时,值域为[an, bn],其中a,b为常数,a1=0, b1=1
(I)若a=1,求数列{an}与数列{bn}的通项公式
(II)若a>0, a≠1,要使数列{bn}是公比不为1的等比数列,求b的值
(III)若a>0,设数列{an}与{bn}的前n项和分别为Sn和Tn,求T2006-S2006的值.
21.(12分)已知定义在R上的函数f(x)满足f(x+y)=f(x)+f(y),当x<0时,f(x)<0
(I)求证f(x)为R上的增函数
(II)当a>2时,解关于x的不等式f(ax2)−2f(x)>f(a2x)−2f(a)
20.(12分)某公司生产的A型商品通过租赁柜台进入某商场销售,第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件,第二年商场开始对该商品征收比率为p%的管理费,(即销售100元要征收p元),于是该商品的定价上升为每件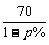 元,预计年销售量将减少p万件
元,预计年销售量将减少p万件
(I)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域。
(II)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收管理费的比率p%的范围是多少?
(III)第二年商场在所征收的管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
19.(12分)已知向量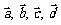 及实数x,y满足
及实数x,y满足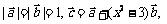
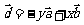 ,若
,若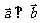 ,
,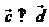 ,且
,且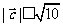
(1)求y关于x的函数关系y=f(x)及其定义域
(2)若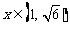 时,不等式
时,不等式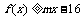 恒成立,求实数m的取值范围
恒成立,求实数m的取值范围
18.(12分)已知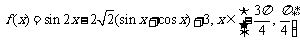 ,若
,若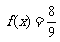 ,求sin2x的值
,求sin2x的值
17.(12分)已知命题P:不等式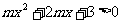 在R上恒成立;命题q:函数
在R上恒成立;命题q:函数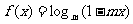 在区间[0,2]是增函数.求实数
在区间[0,2]是增函数.求实数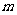 的取值范围,使“P或q”为真命题,“P且q”为假命题.
的取值范围,使“P或q”为真命题,“P且q”为假命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com