
5.函数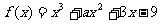 , 已知
, 已知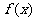 在
在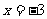 时取得极值, 则
时取得极值, 则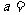 ( )
( )
A. 2 B. 3 C. 4 D. 5
4.设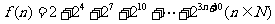 ,则
,则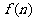 等于 ( )
等于 ( )
A.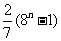 B.
B.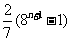 C.
C.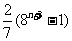 D.
D.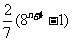
3.已知向量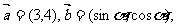 且
且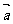 ∥
∥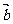 ,则
,则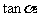 =( )
=( )
A.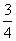 B.
B.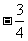 C.
C.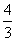 D.
D.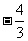
2.设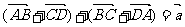 ,而
,而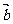 是一非零向量,则下列各结论:①
是一非零向量,则下列各结论:①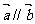 ;②
;②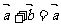 ;③
;③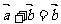 ;④
;④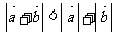 ,其中正确的是( )
,其中正确的是( )
A.①② B.③④ C.②④ D.①③
1.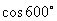 的值是( )
的值是( )
A.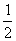 B.-
B.-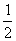 C.
C.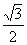 D.-
D.-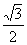
22.(本小题满分14分)
已知数列{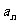 }满足
}满足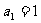 ,
, ,且
,且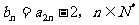 。
。
(Ⅰ)求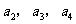 ;
;
(Ⅱ)求证:数列{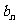 }是以
}是以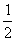 为公比的等比数列,并求其通项公式;
为公比的等比数列,并求其通项公式;
(Ⅲ)设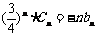 ,记
,记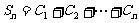 ,求
,求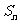 。
。
21.(本小题满分12分)
已知函数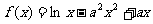
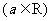 。
。
(Ⅰ)当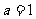 时,证明函数
时,证明函数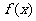 只有一个零点;
只有一个零点;
(Ⅱ)若函数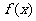 在区间
在区间 上是减函数,求实数
上是减函数,求实数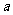 的取值范围。
的取值范围。
20.(本小题满分12分)
甲方是一农场,乙方是一工厂。由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润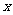 (元)与年产量
(元)与年产量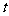 (吨)满足函数关系
(吨)满足函数关系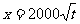 。若乙方每生产一吨产品必须赔付甲方
。若乙方每生产一吨产品必须赔付甲方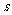 元(以下称
元(以下称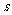 为赔付价格)。
为赔付价格)。
(Ⅰ)将乙方的年利润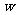 (元)表示为年产量
(元)表示为年产量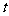 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(Ⅱ)甲方每年受乙方生产影响的经济损失金额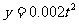 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格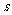 是多少?
是多少?
19.(本小题满分12分)
已知函数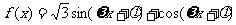
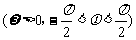 是R上的奇函数,其图像关于直线
是R上的奇函数,其图像关于直线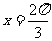 对称,并且在区间[0,
对称,并且在区间[0,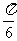 ]上是增函数,求
]上是增函数,求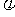 与
与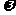 的值。
的值。
18.(本小题满分12分)
设命题p:函数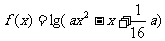 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式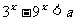 对一切正实数均成立。
对一切正实数均成立。
(Ⅰ)如果p是真命题,求实数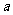 的取值范围;
的取值范围;
(Ⅱ)如果命题“p或q”为真命题,且“p且q”为假命题,求实数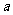 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com