
3.设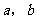 是非零向量,若函数
是非零向量,若函数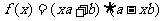 的图像是一条直线,则必有
的图像是一条直线,则必有
A.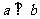 B.
B.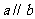 C.
C.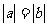 D.
D.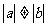
2.设M,N是两个集合,则“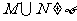 ”是“
”是“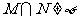 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
1.(理)复数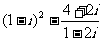 等于
等于
A.0 B.2 C.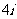 D.
D.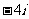
(文)不等式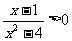 的解集为
的解集为
A.(-2,1) B.(2,+∞)
C.(-2,1)∪(2,+∞) D.(-∞,-2)∪(1,+∞)
22.(本小题满分14分)
已知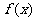 在(-1,1)上有定义,
在(-1,1)上有定义,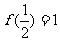 对于
对于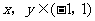 有
有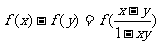 恒成立。对数列
恒成立。对数列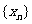 有
有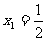 ,
,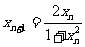
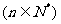 。
。
(1)证明: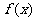 在(-1,1)上为奇函数;
在(-1,1)上为奇函数;
(2)求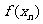 的表达式;
的表达式;
(3)是否存在自然数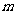 ,使得对于任意
,使得对于任意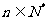 ,
, 恒成立?若存在,求出
恒成立?若存在,求出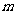 的最小值。
的最小值。
21.(本小题满分12分)
如下图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且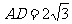 ,BD=CD=2,另一个侧面ABC是正三角形。
,BD=CD=2,另一个侧面ABC是正三角形。
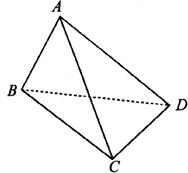
(1)求证:AD⊥BC;
(2)求二面角B-AC-D的大小;
(3)(理)在线段AC上是否存在一点E,使ED与平面BCD成30°角?若存在,确定点E的位置;若不存在,说明理由。
20.(本小题满分12分)
已知函数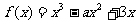 。
。
(1)若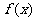 在[1,+∞)上是增函数,求实数
在[1,+∞)上是增函数,求实数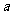 的取值范围;
的取值范围;
(2)若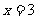 是
是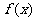 的极值点,求
的极值点,求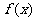 在[1,
在[1,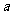 ]上的最小值和最大值。
]上的最小值和最大值。
19.(本小题满分12分)
设F1、F2分别是椭圆C: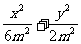 的左、右焦点。
的左、右焦点。
(1)当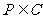 ,且
,且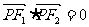 ,
,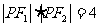 时,求椭圆C的左、右焦点F1、F2;
时,求椭圆C的左、右焦点F1、F2;
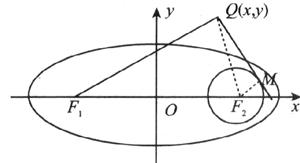
(2)F1、F2是(1)中的椭圆的左、右焦点,已知⊙F2的半径是1,过动点Q的作⊙F2的切线QM,使得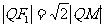 (M是切点),如下图所示,求动点Q的轨迹方程。
(M是切点),如下图所示,求动点Q的轨迹方程。
18.(本小题满分12分)
设向量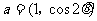 ,
,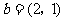 ,
,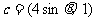 ,
,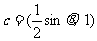 ,其中
,其中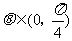 。
。
(1)求 的取值范围;
的取值范围;
(2)若函数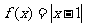 ,比较
,比较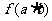 与
与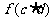 的大小。
的大小。
17.(本小题满分12分)
某射手进行射击时,射中目标的概率为0.7,且各次射击的结果互不影响。
(1)求射手在3次射击中,至多有l次没有击中目标的概率;
(2)求射手第3次击中目标时,恰好射击了4次的概率;
(3)(理)设随机变量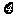 表示射手第3次击中目标时已射击的次数,求
表示射手第3次击中目标时已射击的次数,求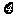 的分布列。
的分布列。
16.(理)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且MN⊥AM,若侧棱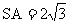 ,则正三棱锥S-ABC外接球的表面积是 。
,则正三棱锥S-ABC外接球的表面积是 。
(文)已知棱长为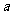 的正四面体ABCD有内切球O,经过该棱锥A-BCD的中截面为M,则O到平面M的距离为 。
的正四面体ABCD有内切球O,经过该棱锥A-BCD的中截面为M,则O到平面M的距离为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com