
2.若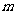 、
、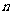 表示直线,
表示直线,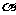 表示平面,则下列命题中,正确的个数为 ( )
表示平面,则下列命题中,正确的个数为 ( )
①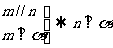 ②
②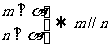 ③
③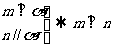 ④
④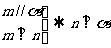
1. 甲:A1、A2是互斥事件;乙:A1、A2是对立事件,那么( )
A. 甲是乙的充分但不必要条件 B. 甲是乙的必要但不充分条件
C. 甲是乙的充要条件 D. 甲既不是乙的充分条件,也不是乙的必要条件
(17)(本小题满分12分)
已知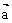 、
、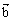 是两个不共线的向量,且
是两个不共线的向量,且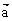 =(4cos
=(4cos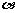 ,3sin
,3sin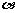 ),
), 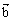 =(3cos
=(3cos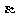 ,4sin
,4sin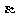 )
)
(Ⅰ)求证: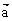 +
+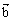 与
与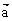 -
-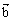 垂直;
垂直;
(Ⅱ)若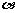 ∈(
∈(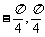 ),
),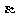 =
=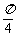 ,且|
,且|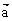 +
+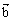 | =
| = 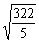 ,求sin
,求sin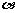 .
.
 (18)(本小题满分12分)
(18)(本小题满分12分)
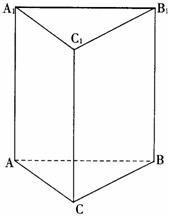
已知:在正三棱柱ABC-A1B1C1中,AB = a,AA1 = 2a . D是侧棱BB1的中点.
求证:(Ⅰ)求证:平面ADC1⊥平面ACC1A1;
(Ⅱ)求平面ADC1与平面ABC所成二面角的大小;
(Ⅲ)求点B到平面ADC1的距离.
(19)(本小题满分12分)
一些零件中有10个合格品与3个次品,安装机器时,从这批零件中任取一个. 各个零件被抽到的可能性相同,如果每次取出的产品都不放回此批产品中,求:
(Ⅰ)直到取出合格品为止时所需抽取次数 的分布列和E
的分布列和E ;
;
(Ⅱ)在取得合格品以前已取出的不合格品数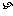 的分布列和E
的分布列和E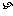 . (精确到0.01)
. (精确到0.01)
(20)(本小题满分12分)
已知点M(x0,f(x1))是函数f(x) =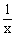 , x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
, x∈(0,+∞)图象C上的一点,记曲线C在点M处的切线为l.
(Ⅰ)求切线l的方程;
(Ⅱ)设l与x轴,y轴的交点分别为A、B,求△AOB周长的最小值.
(21)(本小题满分12分)
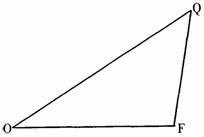
如图,已知:△OFQ的面积为S,且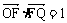 .
.
(Ⅰ)若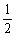 <S<2,求向量
<S<2,求向量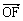 与
与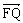 的夹角
的夹角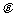 的取值范围;
的取值范围;
 (Ⅱ)设
(Ⅱ)设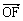 = c(c≥2),S =
= c(c≥2),S =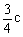 ,若以点O为中心,F为焦点的椭圆经过点Q,当|
,若以点O为中心,F为焦点的椭圆经过点Q,当|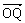 |取得最小值时,求此椭圆方程.
|取得最小值时,求此椭圆方程.
(22)(本小题满分14分)
64个正数排成8行8列,如下所示组成一个数阵
a11 a12 a13 … a18
a21 a22 a23 … a28
a31 a32 a33 … a38
……
a81 a82 a83 … a88
在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数. 已知每一行数都成等差数列,而每一列数都成等比数列(每列公式q都相等)a11 =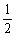 ,a24 = 1,a32 =
,a24 = 1,a32 =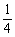
(Ⅰ)求aij的通项公式;
(Ⅱ)记第k行各项和为Ak,求A1的值及Ak通项公式;
(Ⅲ)若Ak<1,求k的值.
(13)不等式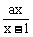 <1的解集为{x | x<1或x>2},那么a的值等于__________.
<1的解集为{x | x<1或x>2},那么a的值等于__________.
(14)已知椭圆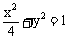 的长轴A1A2,短轴B1B2,将坐标平面沿y轴折成一个二面角,使A1点在平面B1A2B2上的射影恰好是该随圆的一个焦点,则此二面角的大小是__________.
的长轴A1A2,短轴B1B2,将坐标平面沿y轴折成一个二面角,使A1点在平面B1A2B2上的射影恰好是该随圆的一个焦点,则此二面角的大小是__________.
(15)已知(x2 + 2x-3)5 = a10x10 + a9x9 + … + a1x +a0,则a1 = _________.
(16)数学拓展课上,老师定义了一种运算“*”,对于n∈N*满足以下运算性质:(1)2*2 = 1,(2)(2n + 2)* 2 = 3(2n * 2). 则2n*2用含n的代数式表示为 ________.
(1)i100-(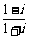 )5 +(
)5 +( )4 = ( )
)4 = ( )
(A)i (B)-i (C)1 (D)1+ i
(2)函数y = x-ln(1+x)的单调递减区间为 ( )
(A)(-∞,-1) (B)(-1,+∞)
(C)(-1,0) (D)(0,+∞)
(3)在等差数列{an}中,a1 + a2 + … + a50 = 200,a51 + a52 + … + a100 = 2700,则a1等于 ( )
(A)-1221 (B)-21.5 (C)-20.5 (D)-20
(4)已知向量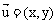 与向量
与向量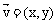 的对应关系记作
的对应关系记作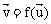 ,那么f
,那么f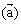 =(2,3)的向量
=(2,3)的向量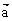 的坐标为 ( )
的坐标为 ( )
(A)(2,1) (B)(1,2) (C)(3,2) (D)(2,3)
(5)设椭圆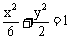 和双曲线
和双曲线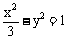 的公共焦点为F1、F2、P为两曲线的一个交点,则cos∠F1PF2的值等于 ( )
的公共焦点为F1、F2、P为两曲线的一个交点,则cos∠F1PF2的值等于 ( )
(A)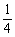 (B)
(B)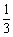 (C)
(C)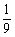 (D)
(D)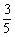
(6)若一个直角所在平面外一点到直角顶点的距离是17,到直角两边的距离是13,则该点到直角所在平面的距离为 ( )
(A)7 (B)8 (C)9 (D)10
|
 是周期为4的偶函数,则f(6.6)= ( )
是周期为4的偶函数,则f(6.6)= ( )
(A)0.36 (B)0.4 (C)0.24 (D)0.6
(8)△ABC的内角A满足sinA + cosA>0,且tanA-sinA<0,则A的取值范围是 ( )
(A)(0,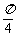 ) (B)(
) (B)(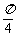 ,
,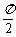 ) (C)(
) (C)(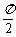 ,
,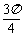 ) (D)(
) (D)(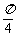 ,
,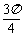 )
)
(9)设n≥2,若an是(1+x)n展开式中含x2的系数,则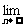 (
(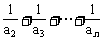 ) = ( )
) = ( )
(A)2
(B)1
(C)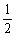 (D)
(D)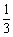
(10)半径为R的球面上,有A、B、C三点,A和B间的球面距离为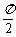 R,A和C、B和C之间的球面距离都是
R,A和C、B和C之间的球面距离都是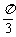 R,则球心O到平面ABC的距离为
( )
R,则球心O到平面ABC的距离为
( )
(A)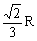 (B)
(B)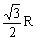 (C)
(C)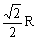 (D)
(D)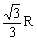
(11)设圆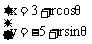 (
(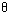 为参数)上有且仅有两点到直线4x-3y = 2的距离等于1,则圆的半径r的取值范围是 ( )
为参数)上有且仅有两点到直线4x-3y = 2的距离等于1,则圆的半径r的取值范围是 ( )
(A)4<r<6 (B)4≤r<6 (C)4<r≤6 (D)4≤r≤6
(12)课程改革后,向100名老师调查对教材新旧版本的态度,有如下结果:赞成旧版本的人数是全体的五分之二,其余的不赞成,赞成新版本的比赞成旧版本的多30人,对新旧版本都赞成的老师数比对新旧版本都不赞成的老师数的3倍多2人,则对新旧版本都赞成的老师人数为 ( )
(A)11 (B)12 (C)13 (D)14
第Ⅱ卷(非选择题共90分 )
20. (本题14分) 已知二次函数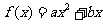 满足条件:
满足条件:
① 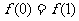 ; ②
; ②  的最小值为
的最小值为 .
.
(1) 求函数 的解析式;
的解析式;
(2) 设数列 的前
的前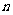 项积为
项积为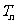 , 且
, 且 , 求数列
, 求数列 的通项公式;
的通项公式;
(3) 在(2)的条件下, 若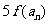 是
是 与
与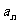 的等差中项, 试问数列
的等差中项, 试问数列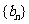 中第几项的值最小? 求出这个最小值.
中第几项的值最小? 求出这个最小值.
19. (本题14分) 用水清洗一堆蔬菜上残留的农药, 对用一定量的水清洗一次的效果作如下假定: 用1个单位量的水可以洗掉蔬菜上残余农药量的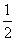 , 用水越多洗掉的农药量也越多, 但总还有农药残留在蔬菜上. 设用
, 用水越多洗掉的农药量也越多, 但总还有农药残留在蔬菜上. 设用 单位量的水清洗一次后, 蔬菜上残留的农药量与单次清洗前残留的农药量之比为函数
单位量的水清洗一次后, 蔬菜上残留的农药量与单次清洗前残留的农药量之比为函数 .
.
(1) 试规定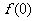 的值, 并解释其实际意义;
的值, 并解释其实际意义;
(2) 试根据假定写出函数 应该满足的条件和具有的主要性质;
应该满足的条件和具有的主要性质;
(3) 设 , 现有
, 现有 单位量的水, 可以清洗一次,
也可以把水平均分成2 份后清洗两次, 试问用哪种方案清洗后蔬菜上残留的农药量比较少? 说明理由.
单位量的水, 可以清洗一次,
也可以把水平均分成2 份后清洗两次, 试问用哪种方案清洗后蔬菜上残留的农药量比较少? 说明理由.
18. (本题14分) 已知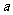 为实数,
为实数, 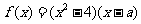 .
.
(1) 求导数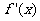 ;
;
(2) 若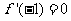 , 求
, 求 在
在 上的最大值和最小值;
上的最大值和最小值;
(3) 若 在
在 和
和 上都是递增的, 求
上都是递增的, 求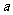 的取值范围.
的取值范围.
17. (本题14分) 已知函数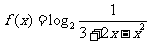 .
.
(1) 求函数 的定义域;
的定义域;
(2) 求证 在
在 上是增函数;
上是增函数;
(3) 求函数 的值域.
的值域.
16. (本题12分) 已知圆 及直线
及直线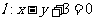 . 当直线
. 当直线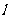 被圆
被圆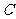 截得的弦长为
截得的弦长为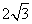 时, 求
时, 求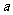 的值, 并求过圆心
的值, 并求过圆心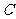 且与直线
且与直线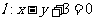 垂直的直线的方程.
垂直的直线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com