
4.过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°则该截面的面积是
A.π B. 2π C. 3π
D. 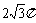
3. 若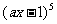 的展开式中
的展开式中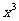 的系数是80,则实数a的值是
的系数是80,则实数a的值是
A.-2 B. 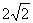 C.
C. 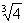 D. 2
D. 2
2.已知向量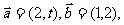 若
若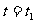 时,
时,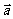 ∥
∥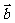 ;
;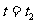 时,
时,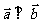 ,则
,则
A.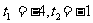 B.
B. 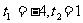
C. 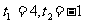 D.
D. 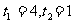
1.函数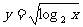 的定义域是
的定义域是
A.(0,1] B. (0,+∞) C. (1,+∞) D. [1,+∞)
21.(本小题满分14分)
已知椭圆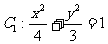 , 抛物线
, 抛物线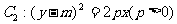 , 且
, 且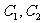 的公共弦
的公共弦
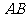 过椭圆
过椭圆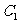 的右焦点 .
的右焦点 .
(Ⅰ) 当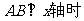 , 求
, 求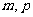 的值, 并判断抛物线
的值, 并判断抛物线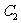 的焦点是否在直线
的焦点是否在直线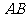 上;
上;
(Ⅱ) 是否存在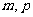 的值, 使抛物线
的值, 使抛物线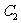 的焦点恰在直线
的焦点恰在直线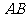 上? 若存在, 求出符合条件的
上? 若存在, 求出符合条件的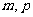 的值; 若不存在, 请说明理由 .
的值; 若不存在, 请说明理由 .
20.(本小题满分14分)
对1个单位质量的含污物体进行清洗, 清洗前其清洁度(含污物体的清洁度定义为:
 为
为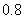 , 要求清洗完后的清洁度为
, 要求清洗完后的清洁度为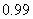 . 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为
. 有两种方案可供选择, 方案甲: 一次清洗; 方案乙: 分两次清洗. 该物体初次清洗后受残留水等因素影响, 其质量变为 . 设用
. 设用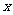 单位质量的水初次清洗后的清洁度是
单位质量的水初次清洗后的清洁度是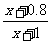
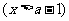 , 用
, 用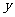 单位质量的水第二次清洗后的清洁度是
单位质量的水第二次清洗后的清洁度是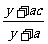 ,
,
其中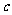
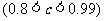 是该物体初次清洗后的清洁度.
是该物体初次清洗后的清洁度.
(Ⅰ)分别求出方案甲以及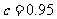 时方案乙的用水量, 并比较哪一种方案用水量较少;
时方案乙的用水量, 并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙, 当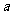 为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论
为某固定值时, 如何安排初次与第二次清洗的用水量, 使总用水量最小? 并讨论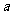 取不同数值时对最少总用水量多少的影响.
取不同数值时对最少总用水量多少的影响.
19.(本小题满分14分)
已知函数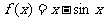 , 数列
, 数列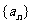 满足:
满足: 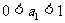 ,
, 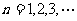
证明 (Ⅰ) 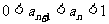 ; (Ⅱ)
; (Ⅱ) 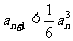 .
.
18. (本小题满分14分)
如图4, 已知两个正四棱锥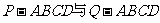 的高分别为1和2,
的高分别为1和2, 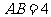
(Ⅰ) 证明:  ;
;
(Ⅱ) 求异面直线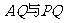 所成的角;
所成的角;
(Ⅲ) 求点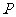 到平面
到平面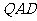 的距离.
的距离.
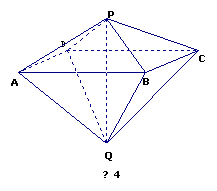
17. (本小题满分12分)
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检), 若安检不合格, 则必须整改. 若整改后经复查仍不合格, 则强制关闭.
设每家煤矿安检是否合格是相互独立的, 且每家煤矿整改前合格的概率是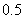 , 整改后安检合格的概率是
, 整改后安检合格的概率是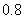 ,
,
计算(结果精确到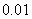 );
);
(Ⅰ) 恰好有两家煤矿必须整改的概率;
(Ⅱ) 平均有多少家煤矿必须整改;
(Ⅲ) 至少关闭一家煤矿的概率 .
16. (本小题满分12分)
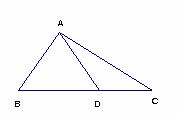
如图3, 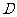 是直角
是直角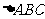 斜边
斜边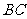 上一点,
上一点, 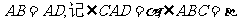 .
.
(Ⅰ)证明: 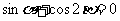 ; (Ⅱ)若
; (Ⅱ)若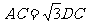 ,求
,求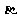 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com