
(17)(本小题满分12分,第一小问满分5分,第二小问满分7分)
已知三点P(5,2)、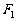 (-6,0)、
(-6,0)、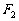 (6,0).
(6,0).
(Ⅰ)求以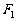 、
、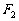 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、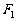 、
、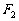 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为 、
、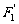 、
、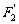 ,求以
,求以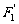 、
、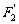 为焦点且过点
为焦点且过点 的双曲线的标准方程。
的双曲线的标准方程。
(18)(本小题满分14分)
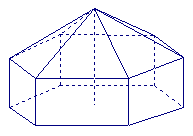
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心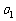 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
(19)(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
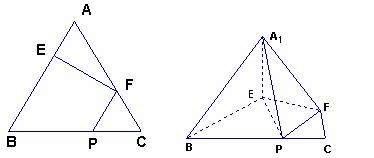
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1)。将△AEF沿EF折起到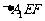 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示)
(20)(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数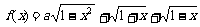 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=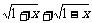 ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足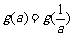 的所有实数a
的所有实数a
(21)(本小题满分14分)
设数列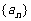 、
、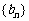 、
、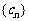 满足:
满足: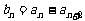 ,
,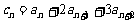 (n=1,2,3,…),
(n=1,2,3,…),
证明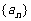 为等差数列的充分必要条件是
为等差数列的充分必要条件是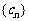 为等差数列且
为等差数列且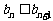 (n=1,2,3,…)
(n=1,2,3,…)
(11)在△ABC中,已知BC=12,A=60°,B=45°,则AC=________
(12)设变量x、y满足约束条件 ,则
,则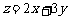 的最大值为________
的最大值为________
(13)今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有______种不同的方法(用数字作答)。
(14)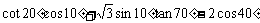 =________
=________
(15)对正整数n,设曲线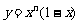 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为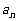 ,则数列
,则数列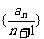 的前n项和的公式是________
的前n项和的公式是________
(16)不等式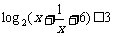 的解集为 _____
的解集为 _____
(1)已知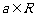 ,函数
,函数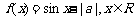 为奇函数,则a=
为奇函数,则a=
(A)0 (B)1 (C)-1 (D)±1
(2)圆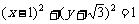 的切线方程中有一个是
的切线方程中有一个是
(A)x-y=0 (B)x+y=0 (C)x=0 (D)y=0
(3)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.已知这组数据的平均数为10,方差为2,则|x-y|的值为
(A)1 (B)2 (C)3 (D)4
(4)为了得到函数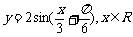 的图像,只需把函数
的图像,只需把函数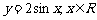 的图像上所有的点
的图像上所有的点
(A)向左平移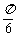 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的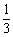 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移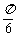 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的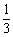 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移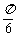 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移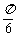 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(5)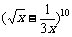 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
(A)0 (B)2 (C)4 (D)6
(6)已知两点M(-2,0)、N(2,0),点P为坐标平面内的动点,满足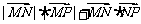 =0,则动点P(x,y)的轨迹方程为
=0,则动点P(x,y)的轨迹方程为
(A)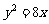 (B)
(B)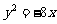 (C)
(C)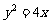 (D)
(D)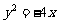
(7)若A、B、C为三个集合,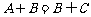 ,则一定有
,则一定有
(A)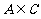 (B)
(B)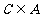 (C)
(C)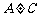 (D)
(D)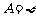
(8)设a、b、c是互不相等的正数,则下列等式中不恒成立的是
(A)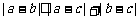 (B)
(B)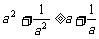
(C)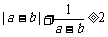 (D)
(D)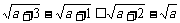
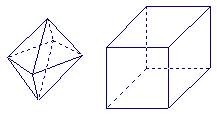
(9)两相同的正四棱锥组成如图1所示的几何体,可放棱长为1的正方体内,使正四棱锥的底面ABCD与正方体的某一个平面平行,且各顶点均在正方体的面上,则这样的几何体体积的可能值有
(A)1个 (B)2个 (C)3个 (D)无穷多个
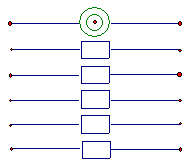
(10)右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时,就能接收到信号,否则就不能接收到信号。若将图中左端的六个接线点随机地平均分成三组,将右端的六个接线点也随机地平均分成三组,再把所有六组中每组的两个接线点用导线连接,则这五个接收器能同时接收到信号的概率是
(A)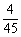 (B)
(B)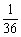 (C)
(C)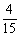 (D)
(D)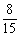
第二卷
21.(本小题满分14分)
已知椭圆C1: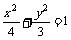 ,抛物线C2:
,抛物线C2: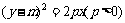 ,且C1、C2的公共弦AB过椭圆C1的右焦点.
,且C1、C2的公共弦AB过椭圆C1的右焦点.
(Ⅰ)当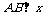 轴时,求p、m的值,并判断抛物线C2的焦点是否在直线AB上;
轴时,求p、m的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)若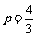 且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程.
且抛物线C2的焦点在直线AB上,求m的值及直线AB的方程.
20.(本小题满分14分)
在m(m≥2)个不同数的排列P1P2…Pn中,若1≤i<j≤m时Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序. 一个排列的全部逆序的总数称为该排列的逆序数. 记排列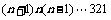 的逆序数为an,如排列21的逆序数
的逆序数为an,如排列21的逆序数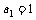 ,排列321的逆序数
,排列321的逆序数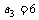 .
.
(Ⅰ)求a4、a5,并写出an的表达式;
(Ⅱ)令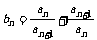 ,证明
,证明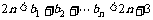 ,n=1,2,….
,n=1,2,….
19.(本小题满分14分)
已知函数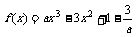 .
.
(I)讨论函数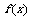 的单调性;
的单调性;
(Ⅱ)若曲线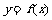 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
18.(本小题满分14分)
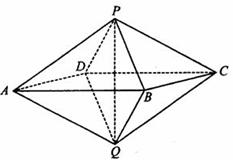
如图2,已知两个正四棱锥P-ABCD与Q-ABCD的高都是2,AB=4.
(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
(Ⅲ)求点P到平面QAD的距离.
17.(本小题满分12分)
某安全生产监督部门对5家小型煤矿进行安全检查(简称安检). 若安检不合格,则必须整改. 若整改后经复查仍不合格,则强制关闭. 设每家煤矿安检是否合格是相互独立的,且每家煤矿整改前安检合格的概率是0.5,整改后安检合格的概率是0.8,计算(结果精确到0.01):
(Ⅰ)恰好有两家煤矿必须整改的概率;
(Ⅱ)某煤矿不被关闭的概率;
(Ⅲ)至少关闭一家煤矿的概率.
16.(本小题满分12分)
已知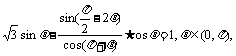 求θ的值.
求θ的值.
15. 若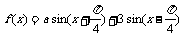 是偶函数,则a= .
是偶函数,则a= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com