
17记函数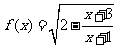 定义域为A,
定义域为A, ,
,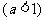 定义域为B。(12分)
定义域为B。(12分)
(1)求A、B
(2)若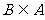 ,求实数的取值范围。
,求实数的取值范围。
18设函数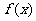
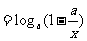 其中
其中 (14分)
(14分)
(1)判断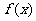 在
在 上的单调性。
上的单调性。
(2)解不等式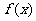
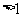 。
。
19已知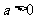 且
且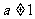 ,设P:函数
,设P:函数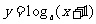 在
在 为减函数。Q:曲线
为减函数。Q:曲线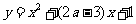 与
与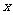 轴有两个不同的交点。若“P且Q”为假,“P或Q”为真,求
轴有两个不同的交点。若“P且Q”为假,“P或Q”为真,求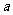 的范围。
的范围。
20某租赁公司拥有汽车100辆,当每辆车月租金为300元时,可全租出,当每辆车月租金每增加50元未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出车每辆每月需维护费用50元。
(1)当每辆车月租金定为3600元时,能租出多少辆车?
(2)每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
21 定义在集合D上的函数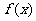 如果同时满足下列条件:①
如果同时满足下列条件:①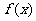 在集合D上单调递减或递增。
在集合D上单调递减或递增。
②存在区间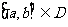 使
使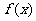 在
在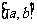 上的值域是
上的值域是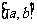 ,那么
,那么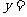
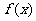 ,
,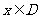 叫做闭函数。
叫做闭函数。
Ⅰ 求闭函数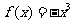 符合条件②的区间
符合条件②的区间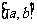 。
。
Ⅱ 判断函数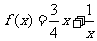 在
在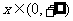 是否是闭函数。
是否是闭函数。
Ⅲ 已知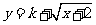 是闭函数,求实数
是闭函数,求实数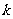 的取值范围。
的取值范围。
11若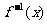 为函数
为函数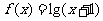 的反函数则
的反函数则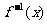 的值域
。
的值域
。
12函数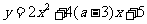 在区间
在区间 上是减函数,则
上是减函数,则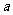 的范围
。
的范围
。
13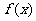 表示
表示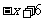 和
和 中较小者,则函数
中较小者,则函数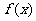 的最大值是
。
的最大值是
。
14函数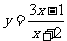 的图像关于
对称。
的图像关于
对称。
15某工厂生产两种成本不同的产品,由于市场销售发生变化,甲产品连续两次提价20%,同时乙产品连续两次降价20%,结果以23.04元售出,这时厂家同时出售甲乙产品各1件,则盈亏情况是 。
16若函数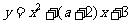 ,在
,在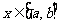 内图像关于
内图像关于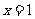 对称,则b=
。
对称,则b=
。
1 已知集合A=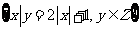 ,B=
,B=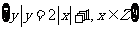 ,则A与B的关系是( )
,则A与B的关系是( )
A A=B B A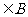 C B
C B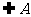 D
D 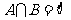
|
|
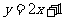 的反函数的图像是( )
的反函数的图像是( )

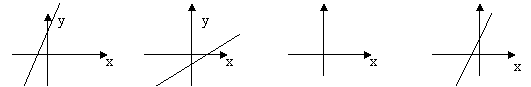
A B C D
3设命题p,q为简单命题,则“p且q”为真是“p或q”为真的( )
A充分不必要条件 B必要不充分条件
C充要条件 D既不充分也非必要条件
4已知函数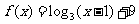 ,若函数y=
,若函数y=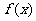 图像与y=g(x)图像关于直线y=x对称,则g(10)的值为( )
图像与y=g(x)图像关于直线y=x对称,则g(10)的值为( )
A1 B4 C10 D11
5已知集合A=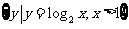 ,B=
,B=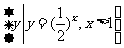 ,则
,则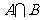 等于( )
等于( )
A  ( 0 , ! ) B ( 0 ,
( 0 , ! ) B ( 0 ,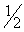 )
C (
)
C (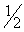 , 1 ) D
, 1 ) D 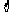
6原命题:“设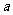 、
、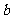 、
、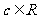 ,若
,若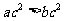 则
则 ”的逆命题、否命题、逆否命题真命题共有( )
”的逆命题、否命题、逆否命题真命题共有( )
A0个 B1个 C2个 D3个
7已知函数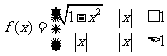 若方程
若方程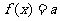 有且只有一个实根,则实数a的取值范围是( )
有且只有一个实根,则实数a的取值范围是( )
A  B
B 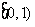 C
C 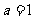 D
D 
8设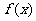 为奇函数,且在
为奇函数,且在 内是减函数,若
内是减函数,若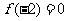 ,则
,则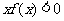 的解集为( )
的解集为( )
A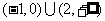 B
B 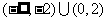 C
C 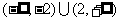 D
D 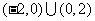
9已知函数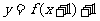 图像经过P
图像经过P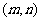 ,则
,则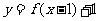 的反函数必经过( )
的反函数必经过( )
A
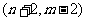 B
B 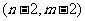 C
C 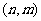 D
D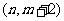
10设函数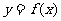 是定义在R上奇函数,且满足
是定义在R上奇函数,且满足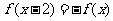 对一切
对一切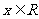 都成立,又当
都成立,又当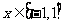 时
时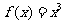 则下列四个命题:①
则下列四个命题:① 函数
函数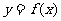 是以4为周期的周期函数②当
是以4为周期的周期函数②当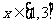 时
时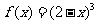 ③函数
③函数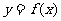 图像的对称轴中有x=1④当
图像的对称轴中有x=1④当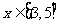 时
时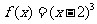
其中正确的命题个数为( )
A1 B2 C3 D4
21.(本小题满分14分)对于函数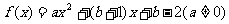 ,若存在实数
,若存在实数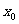 ,使
,使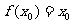 成立,则称
成立,则称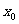 为
为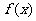 的不动点.⑴当a=2,b=-2时,求
的不动点.⑴当a=2,b=-2时,求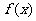 的不动点;
的不动点;
⑵若对于任何实数b,函数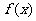 恒有两相异的不动点,求实数a的取值范围;
恒有两相异的不动点,求实数a的取值范围;
⑶在⑵的条件下,若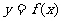 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数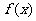 的不动点,且直线
的不动点,且直线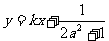 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
20.(本小题满分14分)函数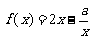 的定义域为(0,1](
的定义域为(0,1](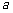 为实数).⑴当
为实数).⑴当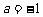 时,求函数
时,求函数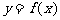 的值域;⑵若函数
的值域;⑵若函数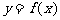 在定义域上是减函数,求
在定义域上是减函数,求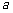 的取值范围;⑶求函数
的取值范围;⑶求函数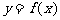 在x∈(0,1]上的最大值及最小值,并求出函数取最值时
在x∈(0,1]上的最大值及最小值,并求出函数取最值时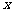 的值.
的值.
19.(本小题满分14分)设函数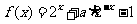 (a为实数).⑴若a<0,用函数单调性定义证明:
(a为实数).⑴若a<0,用函数单调性定义证明: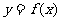 在
在 上是增函数; ⑵若a=0,
上是增函数; ⑵若a=0,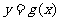 的图象与
的图象与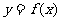 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数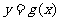 的解析式.
的解析式.
18.(本小题满分14分)已知命题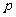 :方程
:方程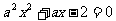 在[-1,1]上有解;命题
在[-1,1]上有解;命题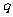 :只有一个实数
:只有一个实数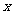 满足不等式
满足不等式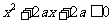 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
17.(本小题满分12分)已知集合A=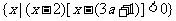 ,B=
,B=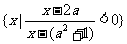 .
.
⑴当a=2时,求A B; ⑵求使B
B; ⑵求使B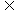 A的实数a的取值范围.
A的实数a的取值范围.
16.(本小题满分12分)二次函数f(x)满足f (x+1)-f (x)=2x且f (0)=1.
⑴求f (x)的解析式;⑵在区间[-1,1]上,y=f (x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
15.如果函数f(x)的定义域为R,对于m,n∈R,恒有f(m+n)=f(m)+f(n)-6,且f(-1)是不大于5的正整数,当x>-1时,f(x)>0.
那么具有这种性质的函数f(x)= .(注:填上你认为正确的一个函数即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com