
(13)不等式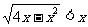 的解集是
.
的解集是
.
(14)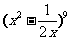 展开式中x9的系数是
.
展开式中x9的系数是
.
(15)在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
(16)如图,一个地区分为5个行政区域,现给地图着色,要求相邻区域不得使用同一颜色,现有4种颜色可供选择,则不同的着色方法共有 种.(以数字作答)

(1)在同一坐标系中,表示直线y=ax与y=x+a,正确的是

(2)已知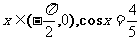 ,则tg 2x=
,则tg 2x=
(A)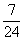 (B)
(B)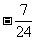 (C)
(C)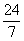 (D)
(D)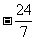
(3)圆锥曲线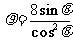 的准线方程是
的准线方程是
(A)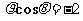 (B)
(B)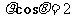 (C)
(C)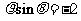 (D)
(D)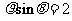
(4)等差数列{an}中,已知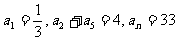 ,则n为
,则n为
(A)48 (B)49 (C)50 (D)51
(5)双曲线虚轴的一个端点为M,两个焦点为F1,F2,∠F1M F2=120°,则双曲线的离心率为
(A)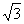 (B)
(B)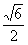 (C)
(C)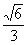 (D)
(D)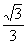
(6)设函数 若f(x0)>1,则x0的取值范围是
若f(x0)>1,则x0的取值范围是
(A)(-1,1) (B)(-1,+∞)
(C)(-∞,-2)∪(0,+∞) (D)(-∞,-1)∪(1,+∞)
(7)函数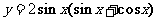 的最大值为
的最大值为
(A)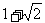 (B)
(B)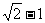 (C)
(C)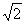 (D)2
(D)2
(8)已知圆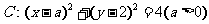 及直线
及直线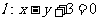 .当直线l被C截得的弦长为
.当直线l被C截得的弦长为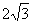 时,则a=
时,则a=
(A)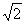 (B)
(B)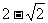 (C)
(C)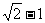 (D)
(D)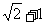
(9)已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是
(A)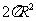 (B)
(B)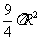 (C)
(C)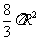 (D)
(D)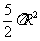
(10)函数f (x)=sinx,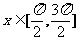 的反函数f-1(x)=
的反函数f-1(x)=
(A)-arcsinx,x∈[-1,1] (B)―π―arcsinx,x∈[-1,1]
(C)π+arcsinx,x∈[-1,1] (D)π-arcsinx,x∈[-1,1]
(11)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1),一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2、P3和P4(入射角等于反射角).设P4的坐标为(x4,0).若1< x4<2,则tgθ的取值范围是
(A)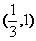 (B)
(B)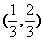 (C)
(C)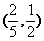 (D)
(D)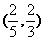
(12)一个四面体的所有棱长都为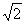 ,四个顶点在同一球面上,则此球的表面积为
,四个顶点在同一球面上,则此球的表面积为
(A)3π
(B)4π (C)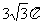 (D)6π
(D)6π
(17)(本小题满分12分)
解不等式:log2(x2-x-2)>log2(2x-2)
(18)(本小题满分12分)
已知函数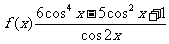 ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
(19)(本小题满分12分)
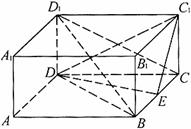
如图,ABCD-A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
(Ⅰ)求三棱锥D1-DBC的体积;
(Ⅱ)证明BD1∥平面C1DE
(Ⅲ)求面C1DE与面CDE所成二面角的正切值.
(20)(本小题满分12分)
设A(-c,0),B(c,0)(c>0)为两定点,动点P到A点的距离与到B点的距离的比为定值a(a>0),求P点的轨迹.
(21)(本小题满分13分)
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费200元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少元?
(22)(本小题满分13分)
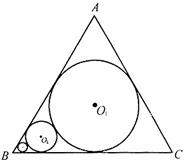
如图,在边长为l的等边△ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB,BC相切,…,圆On+1与On圆外切,且与AB、BC相切,如此无限继续下去,记圆On的面积为an(n∈N)
(Ⅰ)证明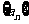 是等比数列.
是等比数列.
(Ⅱ)求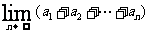 的值.
的值.
(13)函数y=sin2x+1的最小正周期为 .
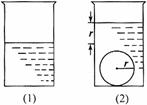
(14)如图,一个底面半径为R的圆柱形量杯中装有适量的水.若放入一个半径为r的实心铁球,水面高度恰好升高r,则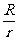 =
.
=
.
(15)在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表,观察表中数据的特点,用适当的数填入表中空白( )内.
|
年龄(岁) |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
|
收缩压(水银柱 毫米) |
110 |
115 |
120 |
125 |
130 |
135 |
( ) |
145 |
|
舒张压(水银柱 毫米) |
70 |
73 |
75 |
78 |
80 |
83 |
( ) |
88 |
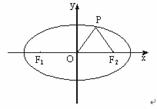
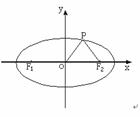
(16)如图,F1,F2分别为椭圆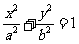 的左、右焦点,点P在椭圆上,△POF2是面积为
的左、右焦点,点P在椭圆上,△POF2是面积为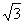 的正三角形,则b2的值是
.
的正三角形,则b2的值是
.
(1)设a,b,c,d∈R,且a>b,c>d,则下列结论中正确的是
(A)a+c>b+d (B)a-c>b-d (C)ac>bd (D)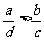
(2)设M和m分别表示函数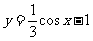 的最大值和最小值,则M+m等于
的最大值和最小值,则M+m等于
(A)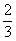 (B)
(B)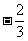 (C)
(C)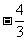 (D)-2
(D)-2
(3)若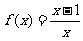 ,则方程f(4x)=x的根是
,则方程f(4x)=x的根是
(A)-2 (B)2 (C)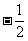 (D)
(D)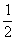
(4)若集合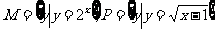 ,则MP=
,则MP=
(A)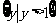 (B)
(B)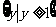
(C)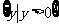 (D)
(D)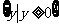
(5)若A,B,C是△ABC的三个内角,且A<B<C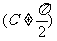 ,则下列结论中正确的是
,则下列结论中正确的是
(A)tanA<tanC (B)ctanA<ctanC
(C)sinA<sinC (D)cosA<cosC
(6)在等差数列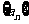 中,已知a1+a2+a3+a4+a5=20,那么a3等于
中,已知a1+a2+a3+a4+a5=20,那么a3等于
(A)4 (B)5 (C)6 (D)7
(7)设复数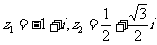 ,则
,则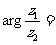
(A)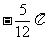 (B)
(B)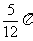 (C)
(C)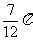 (D)
(D)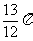
(8)函数f(x)=∣x∣和g(x)=x(2-x)的递增区间依次是
(A)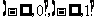 (B)
(B)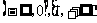
(C)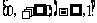 (D)
(D)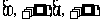
(9)在同一坐标系中,方程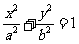 与ax+by2=0(a>b>0)的曲线大致是
与ax+by2=0(a>b>0)的曲线大致是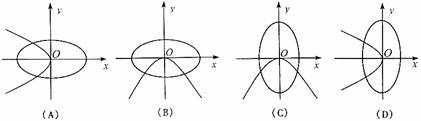
(10)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个新节目插入原节目单中,且两个新节目不相邻,那么不同插法的种数为
(A)6 (B)12 (C)15 (D)30
(11)如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H,I,J分别为AF,AD,BE,DE的中点,将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成的角的度数为
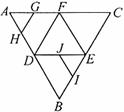
(A)90° (B)60° (C)45° (D)0°
(12)已知直线ax+by+c=0(abc≠0)与圆x2+y2=1相切,则三条边长分别为∣a∣, ∣b∣,∣c∣的三角形
(A)是锐角三角形 (B)是直角三角形
(C)是钝角三角形 (D)不存在
第Ⅱ卷
(17)(本小题满分12分)
解不等式: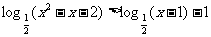 .
.
(18)(本小题满分12分)
已知函数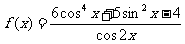 ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
(19)(本小题满分12分)
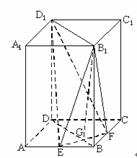
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为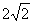 ,侧棱长为4.E,F分别为棱AB,BC的中点,
,侧棱长为4.E,F分别为棱AB,BC的中点, .
.
(Ⅰ)求证:平面B1EF⊥平面BDD1B1;
(Ⅱ)求点D1到平面B1EF的距离d;
(Ⅲ)求三棱锥B1-EFD1的体积V.
(20)(本小题满分12分)
某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护需50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
(21)(本小题满分13分)
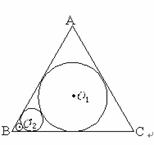
如图,在边长为l的等边△ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB,BC相切,…,圆On+1与圆On外切,且与AB,BC相切,如此无限继续下去.记圆On的面积为an(n∈N).
(Ⅰ)证明{an}是等比数列;
(Ⅱ)求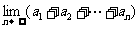 的值.
的值.
(22)(本小题满分13分)
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为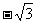 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
(ⅰ)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ⅱ)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
13)如图,一个底面半径为R的圆柱形量杯中装有适量的水.若放入一个半径为r的实心铁球,水面高度恰好升高r,则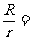 ____________.
____________.
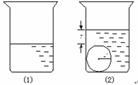
(14)在某报《自测健康状况》的报道中,自测血压结果与相 应年龄的统计数据如下表,观察表中数据的特点,用适当的数填入表中空白(____)内.
|
年龄(岁) |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
|
收缩压(水银柱 毫米) |
110 |
115 |
120 |
125 |
130 |
135 |
(___) |
145 |
|
舒张压(水银柱 毫米) |
70 |
73 |
75 |
78 |
80 |
83 |
(___) |
88 |
(15)如图,F1,F2分别为椭圆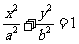 的左、右焦点,点P在椭圆上△POF2是面积为
的左、右焦点,点P在椭圆上△POF2是面积为
 的正三角形,则b2的值是_________________.
的正三角形,则b2的值是_________________.
(16)若存在常数p>0,使得函数f(x)满足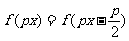 (x∈R),则f(x)的一个正周期为_____________.
(x∈R),则f(x)的一个正周期为_____________.
(1)若集合M={y | y=2-x},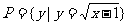 ,则
,则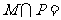
A.{y|y>1} B.{y|y≥1} C.{y|y>0} D.{y|y≥0}
(2)若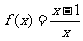 ,则方程f(4x)=x的根是
,则方程f(4x)=x的根是
(A)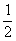 (B)
(B)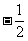 (C)
(D)-2
(C)
(D)-2
(3)设复数z1=-1+i,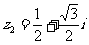 ,则
,则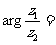
(A)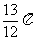 (B)
(B)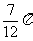 (C)
(C)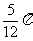 (D)
(D)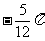
(4)函数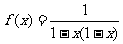 的最大值是
的最大值是
(A)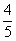 (B)
(B)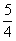 (C)
(C)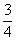 (D)
(D)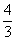
(5)在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a>b>0)的曲线大致是
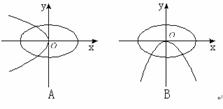
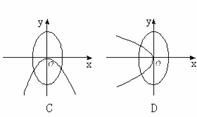
(6)若A,B,C是△ABC的三个内角,且A<B<C(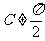 ),则下列结论中正确的是
),则下列结论中正确的是
(A)sinA<sinC (B)cosA<cosC
(C)tanA<tanC (D)cotA<cotC
(7)椭圆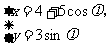 (为参数)的焦点坐标为
(为参数)的焦点坐标为
(A)(0,0),(0,-8) (B)(0,0),(-8,0)
(C)(0,0),(0,8) (D)(0,0),(8,0)
(8)如图,在正三角形ABC中,D,E,F分别为各边的中点, G,H,I,J分别为AF,AD,BE,DE的中点.将△ABC沿DE,EF, DF折成三棱锥以后,GH与IJ所成角的度数为
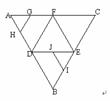 (A)90° (B)60° (C)45° (D)0°
(A)90° (B)60° (C)45° (D)0°
(9)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原节目单中,那么不同插法的种数为
(A)42 (B)30 (C)20 (D)12
(10)已知直线ax+by+c=0(abc≠0)与圆x2+y2=1相切,则三条边长分别为| a |,| b |,| c |的三角形
(A)是锐角三角形 (B)是直角三角形
(C)是钝角三角形 (D)不存在
(11)若不等式| ax+2 | < 6的解集为(-1,2),则实数a等于
(A)8 (B)2 (C)-4 (D)-8
(12)在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为x=0,y=0,2x+3y=30,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是
(A)95 (B)91 (C)88 (D)75
第Ⅱ卷
22.(本小题满分12分)
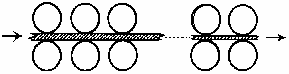
上图为一台冷轧机的示意图;冷轧机由若干对轧辊组成。带钢从一端输人,经过各对轧辊逐步减薄后输出。
(1)输入带钢的厚度为a,输出带钢的厚度为β,若每对轧辊的减薄率不超过ro,问冷轧机至少需要安装多少对轧辊?
(一对辊减薄率=输入该对的带钢厚度-从该对输出的带钢厚度)输入该对的带钢厚度
21.本小题满分12分
已知正四棱柱ABCD-A1B1C1D1,点E在棱D1D上,截面EACD1B,且面EAC与底面ABcD所成的角为45°,AB=a
(Ⅰ)求截而EAC的面积:
(Ⅱ)求异面直线A1B1与AC之间的距离;
(Ⅲ)求三棱锥B1-EAC的体积
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com