
4.若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象
A.关于直线y=x对称 B.关于x轴对称 C.关于y轴对称 D.关于原点对称
3.映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为“满射”.已知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为
A.24 B.6 C. 36 D.72
2.设A、B是两个集合,定义A-B={x|x∈A,且x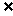 B},若M={x||x+1|≤2},N={x|x=|sinα|,α∈R},则M-N=
B},若M={x||x+1|≤2},N={x|x=|sinα|,α∈R},则M-N=
A.[-3,1] B.[-3,0] C.[0,1] D.[-3,0)
1.设集合P={3,4,5},Q={4,5,6,7},定义P※Q={(a,b)|a∈P,b∈Q},则P※Q中元素的个数为
A.3 B.4 C.7 D.12
20.已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|;
(Ⅲ)若h(x)=g(x)-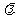 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数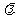 的取值范围。
的取值范围。
19.设函数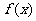 的定义域为R,对任意实数
的定义域为R,对任意实数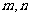 恒有
恒有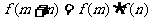 ,且当
,且当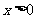 时,
时,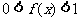 。(1)求证:
。(1)求证: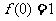 且当
且当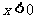 时,
时,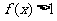 ;
;
(2)求证: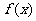 在R上单调递减;
在R上单调递减;
(3)若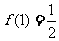 ,试解不等式:
,试解不等式: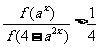 (
( 且
且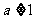 )
)
18.已知函数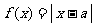 ,
,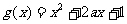 (
(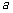 为正常数),且函数
为正常数),且函数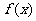 与
与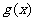 的图象在
的图象在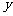 轴上的截距相等。⑴求
轴上的截距相等。⑴求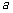 的值;⑵求函数
的值;⑵求函数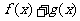 的单调递增区间。
的单调递增区间。
17.已知f(x)=x2-x+k,若log2f(a)=2且f(log2a)=k(a>0且a≠1)。
⑴确定k的值;⑵求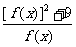 的最小值及对应的x值。
的最小值及对应的x值。
16.设命题p:函数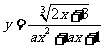 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式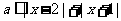 对一切实数
对一切实数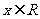 均成立。如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围。
均成立。如果命题p或q为真命题,命题p且q为假命题,求实数a的取值范围。
15.设函数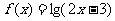 的定义域为集合M,函数
的定义域为集合M,函数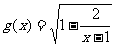 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合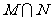 ,
,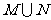 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com