
20.(本小题满分12分)
把正奇数数列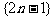 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设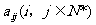 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第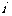 行、从左往右数第
行、从左往右数第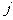 个数。
个数。
(I)若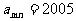 ,求
,求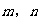 的值;
的值;
(II)已知函数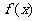 的反函数为
的反函数为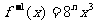
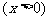 ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为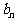 ,求数列
,求数列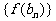 的前n项和
的前n项和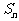 。
。
19.(本小题满分14分)
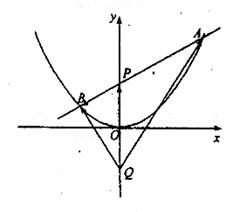
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A、B两点,点Q是点P关于原点的对称点。
(Ⅰ)设点P分有向线段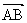 所成的比为λ,证明
所成的比为λ,证明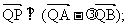
(Ⅱ)设直线AB的方程是x-2y+12=0,过A、B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程。
18.(本小题满分14分)
已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.求:
(Ⅰ)A、B两组中有一组恰有两支弱队的概率;
(Ⅱ)A组中至少有两支弱队的概率.
17. (本小题满分14分)
(本小题满分14分)
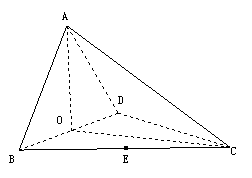
如图,四面体ABCD中,O、E分别是BD、BC的中点,
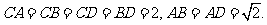
(I)求证: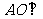 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
16.(本小题满分12分)
已知 |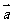 |=1,|
|=1,|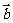 |=
|=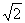 ,(I)若
,(I)若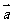 //
//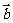 ,求
,求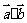 ; (II)若
; (II)若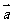 ,
,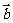 的夹角为135°,求 |
的夹角为135°,求 |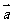 +
+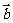 | .
| .
15.(本小题满分14分)
已知函数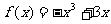
(I)证明:函数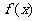 是奇函数;
是奇函数;
(II)求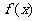 的单调区间。
的单调区间。
14.设函数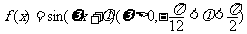 ,给出以下四个论断:
,给出以下四个论断:
①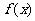 的周期为π; ②
的周期为π; ②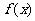 在区间(-
在区间(-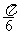 ,0)上是增函数;
,0)上是增函数;
③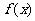 的图象关于点(
的图象关于点(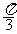 ,0)对称; ④
,0)对称; ④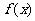 的图象关于直线
的图象关于直线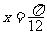 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
 (只需将命题的序号填在横线上).
(只需将命题的序号填在横线上).
13.圆C: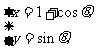 (
(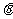 为参数)的普通方程为__________,设O为坐标原点,
为参数)的普通方程为__________,设O为坐标原点,
点M(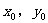 )在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。
)在C上运动,点P(x,y)是线段OM的中点,则点P的轨迹方程为________________。
12.与直线2x-y-4=0平行且与曲线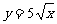 相切的直线方程是 .
相切的直线方程是 .
11.一个正四棱锥的底面边长为2,侧棱长为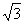 ,五个顶点都在同一个球面上,则此
,五个顶点都在同一个球面上,则此
球的表面积为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com