
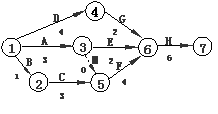
4.某工程的工序流程图如右图所示(工时数单位:天),则
工程总时数为 天。
3.函数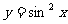 的最小正周期为 .
的最小正周期为 .
2.
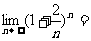 .
.
1.已知集合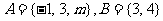 ,若
,若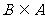 ,则实数
,则实数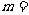 .
.
22.(本题满分18分.第(1)题4分,第(2)题6分,第(3)题8分)
(1)若等比数列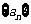 的前
的前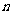 项和为
项和为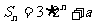 ,求实数
,求实数 的值;
的值;
(2)对于非常数数列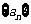 有下面的结论:若数列
有下面的结论:若数列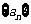 为等比数列,则该数列的前n项和为
为等比数列,则该数列的前n项和为
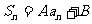 (A,B为常数).写出它的逆命题并判断真假,请说明理由.
(A,B为常数).写出它的逆命题并判断真假,请说明理由.
(3)若数列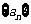 为等差数列,则该数列的前n项和为
为等差数列,则该数列的前n项和为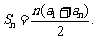 对其逆命题进行研究,写出你的结论,并说明理由.
对其逆命题进行研究,写出你的结论,并说明理由.
[解]
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
已知函数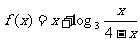 .
.
(1)求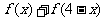 的值;
的值;
(2)猜测函数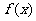 的图象具备怎样的对称性,并给出证明;
的图象具备怎样的对称性,并给出证明;
(3)若函数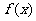 的图象与直线
的图象与直线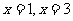 及
及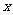 轴所围成的封闭图形的面积为
轴所围成的封闭图形的面积为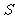 ,求
,求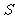 的值.
的值.
[解]
20.(本题满分14分,第(1)题4分,第(2)题10分)
已知函数 的图像与
的图像与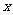 轴正半轴的交点为
轴正半轴的交点为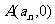 ,
,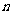 =1,2,3,….
=1,2,3,….
(1)
求数列 的通项公式;
的通项公式;
(2)
令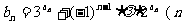 为正整数), 问是否存在非零整数
为正整数), 问是否存在非零整数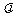 , 使得对任意正整数
, 使得对任意正整数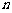 ,都有
,都有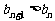 ? 若存在, 求出
? 若存在, 求出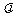 的值 , 若不存在 , 请说明理由.
的值 , 若不存在 , 请说明理由.
[解]
19.(本题满分14分,第(1)题8分,第(2)题6分)
据市场调查,某种商品一年内每件出厂价在6千元的基础上,按月呈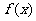
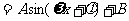 的模型波动(
的模型波动(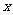 为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为
为月份),已知3月份达到最高价8千元,7月份价格最低为4千元,该商品每件的售价为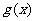 (
(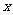 为月份),且满足
为月份),且满足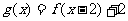 .
.
(1)分别写出该商品每件的出厂价函数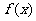 、售价函数
、售价函数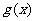 的解析式;
的解析式;
(2)问哪几个月盈利?
18.(本题满分12分,第(1)题4分,第(2)题8分)
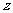 为一元二次方程
为一元二次方程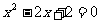 的一个根,且
的一个根,且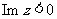 .
.
(1)求复数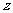 ;
;
(2)若实数 满足不等式
满足不等式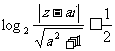 ,求
,求 的取值范围.
的取值范围.
[解]
17.(本题满分12分)
已知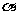 为锐角,
为锐角,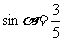 ,
, 是第四象限角,
是第四象限角,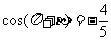 .
.
求 的值.
的值.
[解]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com