
6. 已知函数
已知函数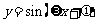
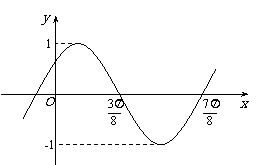
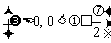 ,且此函数的图象如图所示,则点
,且此函数的图象如图所示,则点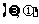 的坐标是( )
的坐标是( )
(A) 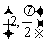 (B)
(B)
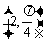
(C)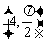 (D)
(D) 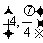
5.某台机器上安装甲乙两个元件,这两个元件的使用寿命互不影响.已知甲元件的使用寿命超过1年的概率为0.6,要使两个元件中至少有一个的使用寿命超过1年的概率至少为0.9,则乙元件的使用寿命超过1年的概率至少为( )
(A) 0.3 (B) 0.6 (C) 0.75 (D) 0.9
4.已知直线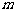 、
、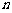 、
、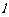 ,平面
,平面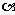 、
、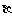 ,有下列命题:
,有下列命题:
①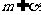 、
、 ;
;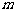 ∥
∥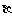 ,
,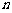 ∥
∥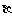 ,则
,则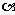 ∥
∥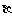
②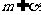 、
、 ;
;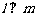 ,
,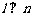 ,则
,则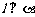
③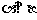 ,
,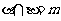 ,
,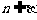 ,
,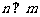 ,则
,则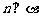
④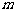 ∥
∥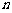 ,
, ,则
,则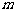 ∥
∥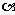
其中正确的命题是:( )
(A) ①③ (B) ②④ (C) ①②④ (D)③
3.设集合A={1,2,3,4},m、n∈A,则方程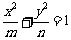 表示焦点位于x轴上的椭圆有( )
表示焦点位于x轴上的椭圆有( )
(A)6个 (B)8个 (C)12个 (D)16个
2.已知抛物线的方程为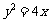 ,则此抛物线的焦点坐标为( )
,则此抛物线的焦点坐标为( )
(A)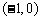 (B)
(B) 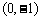 (C)
(C) 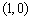 (D)
(D) 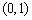
1.已知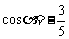 ,则
,则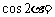 ( )
( )
(A)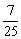 (B)
(B) 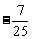 (C)
(C) 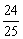 (D)
(D)
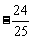
20.(本小题14分)
对于数列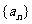 ,定义数列
,定义数列 为
为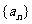 的“差数列”.
的“差数列”.
(I)若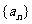 的“差数列”是一个公差不为零的等差数列,试写出
的“差数列”是一个公差不为零的等差数列,试写出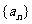 的一个通项公式;
的一个通项公式;
(II)若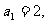
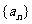 的“差数列”的通项为
的“差数列”的通项为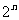 ,求数列
,求数列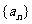 的前n项和
的前n项和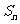 ;
;
(III)对于(II)中的数列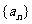 ,若数列
,若数列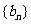 满足
满足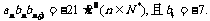
求:①数列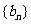 的通项公式;②当数列
的通项公式;②当数列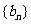 前n项的积最大时n的值.
前n项的积最大时n的值.
19.(本小题满分14分)
设 ,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
(I)求点M的轨迹C的方程;
(II)设直线BF与曲线C交于P,Q两点,证明:向量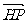 、
、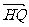 与
与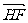 的夹角相等.
的夹角相等.
18.(本小题13分)
如图,ABCD-A1B1C1D1是正四棱柱,则棱长为3,底面边长为2,E是棱BC的中点.
 (I)求证:BD1∥平面C1DE;
(I)求证:BD1∥平面C1DE;
(II)求二面角C1-DE-C的大小;
(III)在侧棱BB1上是否存在点P,
使得CP⊥平面C1DE?证明你的结论.
17.(本小题满分13分)
设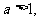 函数
函数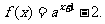
(I)求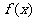 的反函数
的反函数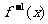 ;
;
(II)若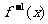 在[0,1]上的最大值与最小值互为相反数,求a的值;
在[0,1]上的最大值与最小值互为相反数,求a的值;
(III)若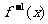 的图象不经过第二象限,求a的取值范围.
的图象不经过第二象限,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com