
9.已知函数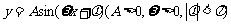 的图象如下图所示,则函数的解析式为
( )
的图象如下图所示,则函数的解析式为
( )


 A.
A.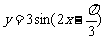 B.
B.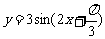
C.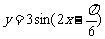 D.
D.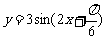
8.已知向量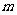 =(1,1),
=(1,1),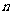 与
与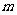 的夹角为
的夹角为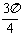 且
且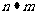
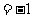 ,则向量
,则向量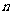 = ( )
= ( )
A. (-1,0) B. (0,-1) C.(-1,0)或(0,-1) D. (-1,-1)
7.已知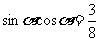 且
且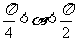 ,则
,则 的值是
( )
的值是
( )
A.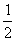 B.
B.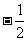 C.
C.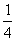 D.
D.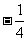
6.已知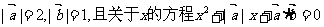 有实根,则
有实根,则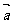 与
与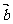 夹角的取值
夹角的取值
范围是 ( )
A.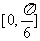 B.
B.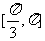 C.
C.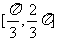 D.
D.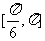
5.数列{an}的通项式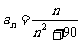 ,则数列{an}中的最大项是
( )
,则数列{an}中的最大项是
( )
A.第9项 B.第8项和第9项
C.第10项 D.第9项和第10项
4.设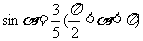 ,
,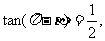 则
则 ( )
( )
A.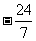 B.
B.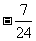 C.
C.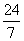 D.
D.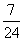
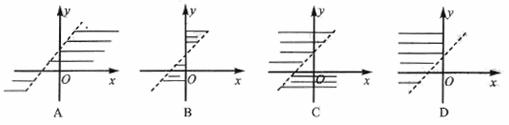
3.不等式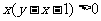 表示的平面区域是
( )
表示的平面区域是
( )
2. .函数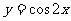 在下列哪个区间上是减函数
( )
在下列哪个区间上是减函数
( )
A.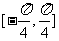 B.
B.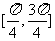 C.
C.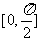 D.
D.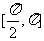
1.一个等差数列共n项,其和为90,这个数列的前10项的和为25,后10项的和为75,则项数n为 ( )
A.14 B.16 C.18 D.20
(17)(本小题满分12分)
设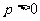 ,二项式
,二项式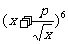 的展开式中的常数项不大于第三项的系数,求
的展开式中的常数项不大于第三项的系数,求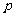 的取值范围。
的取值范围。
(18)(本小题满分l2分)
观察下列各式: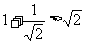 ,
,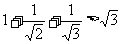 ,
,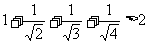 ,……请你归纳出一个一般结论,并用数学归纳法证明。
,……请你归纳出一个一般结论,并用数学归纳法证明。
(19)(本小题满分12分)
已知10件产品中包含2件次品,今在其中任取两件。
(I)已知取出的两件中有一件是次品,求另一件也是次品的概率;
(Ⅱ)求取出的次品个数的分布列和数学期望.
(20)(本小题满分l2分)
函数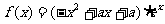 (
(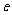 为自然对数的底)。
为自然对数的底)。
(I)当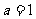 时,求
时,求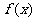 在[0,2]上的最大值与最小值;
在[0,2]上的最大值与最小值;
(Ⅱ)求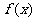 的单调递增区间。
的单调递增区间。
(21)(本小题满分12分)
甲、乙、丙三人独立地破译一个密码。已知甲能破译的概率为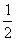 ,甲、乙都能破译的概率为
,甲、乙都能破译的概率为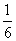 ,乙、丙都不能破译的概率为
,乙、丙都不能破译的概率为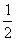 。
。
(I)求乙、丙各自能破译的概率;
(Ⅱ)要使密码被破译的概率不低于99.9%,至少需要与甲同等水平的人多少个?
(III)密码被破译的人数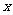 是一个随机变量,求
是一个随机变量,求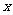 的分布列及期望值。
的分布列及期望值。
(22)(本小题满分14分)
已知 ,
,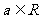 ,函数
,函数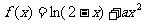 。
。
(I)设曲线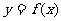 在点
在点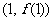 处的切线为直线
处的切线为直线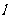 ,若直线
,若直线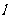 与圆
与圆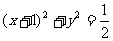 相切,求
相切,求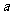 的值;
的值;
(Ⅱ)若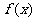 在区间(0,2)上是减函数,求实数
在区间(0,2)上是减函数,求实数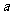 的取值范围;
的取值范围;
(Ⅲ)对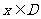 ,如果函数
,如果函数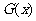 的图象在函数
的图象在函数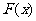 的下方,则称函数
的下方,则称函数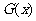 的区间D上被函数
的区间D上被函数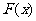 覆盖。求证:当
覆盖。求证:当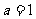 时,函数
时,函数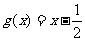 在区间
在区间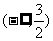 上被
上被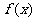 覆盖。
覆盖。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com