
7.连接抛物线x2=4y的焦点F与点M(1,0)所得的线段与抛物线交于点A,设点O为坐标原点,则三角形OAM的面积为
A.-1+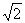 B.
B.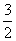 -
-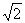 C.1+
C.1+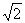 D.
D.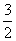 +
+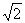
6.一袋中装有大小相同,编号分别为1,2,3,4,5,6,7,8的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为
A.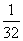 B.
B.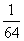 C.
C.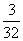 D.
D.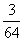
5.设(x2+1)(2x+1)9=a0+a1(x+2)+a2(x+2)2+…+a11(x+2)11,则a0+a1+a2+…+a11的值为
A.-2 B.-1 C.1 D.2
4.若tanα=3,tanβ=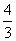 ,则tan(α-β)等于
,则tan(α-β)等于
A.-3
B.-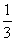 C.3 D.
C.3 D.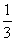
3.函数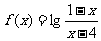 的定义域为
的定义域为
A.(1,4) B.[1,4)
C.(-∞,1)∪(4,+∞) D.(-∞,1]∪(4,+∞)
2.函数y=5tan(2x+1)的最小正周期为
A.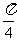 B.
B.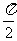 C.π
D.2π
C.π
D.2π
1.若集合M={0,1},I={0,1,2,3,4,5},则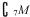 为
为
A.{0,1} B.{2,3,4,5}
C.{0,2,3,4,5} D.{1,2,3,4,5}
21.(本小题满分l4分)
已知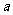 是实数,函数
是实数,函数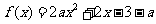 .如果函数
.如果函数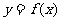 在区间
在区间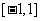 上有零点,求
上有零点,求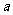 的取值范围.
的取值范围.
20.(本小题满分14分)
已知函数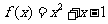 ,
,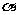 、
、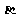 是方程
是方程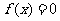 的两个根(
的两个根(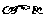 ),
),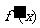 是
是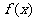 的导数设
的导数设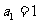 ,
,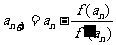 ,
,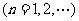 .
.
(1)求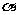 、
、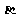 的值;
的值;
(2)已知对任意的正整数 有
有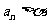 ,记
,记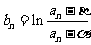 ,
,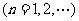 .求数列{
.求数列{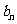 }的前
}的前 项和
项和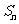 .
.
19.(本小题满分14分)
在平面直角坐标系 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为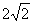 的圆
的圆 与直线
与直线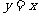 相切于坐标原点
相切于坐标原点 .椭圆
.椭圆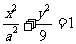 与圆
与圆 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为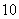 .
.
(1)求圆 的方程;
的方程;
(2)试探究圆 上是否存在异于原点的点
上是否存在异于原点的点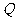 ,使
,使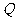 到椭圆右焦点F的距离等于线段
到椭圆右焦点F的距离等于线段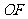 的长.若存在,请求出点
的长.若存在,请求出点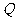 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com