
2.复数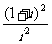 = ( )
= ( )
A.2 B.-2 C.-2i D.2i
1.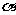 是第一象限角,
是第一象限角,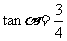 ,则
,则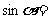 ( )
( )
A.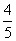 B.
B.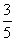 C.
C.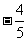 D.
D.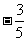
20.(本小题满分16分)
已知a为实数,函数f(x)=x2-2alnx.
(Ⅰ)求f(x)在[1,+∞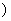 上的最小值g(a);
上的最小值g(a);
(Ⅱ)若a>0,试证明“方程f(x)=2ax有唯一解”的充要条件是“a=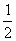 ”.
”.
19.(本小题满分16分)
某工厂统计资料显示,一年中总产品次品率P与日产量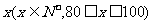 件之间的关系如下表所示:
件之间的关系如下表所示:
日产量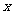 |
80 |
81 |
82 |
… |
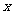 |
… |
98 |
99 |
100 |
次品率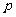 |
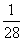 |
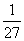 |
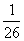 |
… |
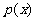 |
… |
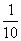 |
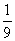 |
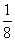 |
其中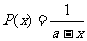 (a为常数),已知生产一件正品赢利k元,生产一件次品损失
(a为常数),已知生产一件正品赢利k元,生产一件次品损失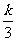 元
元
(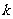 为给定常数).
为给定常数).
(Ⅰ)求出a,并将该厂的日盈利额y(元)表示为日生产量x(件)的函数;
(Ⅱ)为获取最大盈利,该厂的日生产量应定为多少件?
18.(本小题满分15分)
在平面直角坐标系中,直线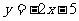 上有一系列点:
上有一系列点: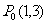 ,
,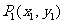 ,
,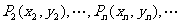 ,已知数列
,已知数列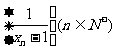 是首项为
是首项为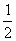 ,公差为1的等差数列.
,公差为1的等差数列.
(Ⅰ)求数列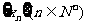 及数列
及数列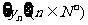 的通项公式;
的通项公式;
(Ⅱ)是否在一个半径最小的圆C,使得对于一切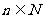 ,点
,点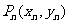 均在此圆的内部(包括圆周)?若存在,求由此方程;若不存在,请说明理由.
均在此圆的内部(包括圆周)?若存在,求由此方程;若不存在,请说明理由.
17.(本小题满分15分)
已知中心在原点O,焦点在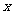 轴上的椭圆C离心率为
轴上的椭圆C离心率为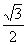 ,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为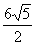 .
.
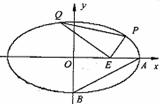
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点E(3,0),设点P、Q是椭圆上的两个动点,满足EP⊥EQ,求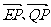 的取值范围.
的取值范围.
16.(本小题满分14分)
已知四边形ABCD的等腰梯形,AB=3,DC=1,∠BAD=45°,DE⊥AB(如图1)现将△ADE沿DE折起,使得AE⊥EB(如图2),连结AC、AB、设M是AB的中点.
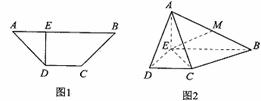
(Ⅰ)求证:BC⊥平面AEC;
(Ⅱ)判断直线EM是否平行平面ACD,并说明理由.
15.(本小题满反4分)
在△ABC中,已知a、b、c分别是角A、B、C的对边,不等式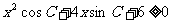
对一切实数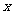 恒成立.
恒成立.
(Ⅰ)求角C的最大值;
(Ⅱ)若角C取得最大值,且a = 2b,求角B的大小.
14.水管或煤气的外部京城需要包扎,以便对管道起保护作用,包扎时用很长的带子缠绕在管道外部,若要使带子全部包住管道且没有重叠的部分(不考虑管子两端的情况,如图所示),这就要精确计算带子的“缠绕角度”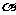 (
(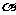 指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面母线的一部分),若带子宽度为1,水管直径为2,则“缠绕角度”
指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面母线的一部分),若带子宽度为1,水管直径为2,则“缠绕角度”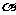 的余弦值为
.
的余弦值为
.
13.观察下列算式,猜测由此表提供的一般法则,用适当的数学式子表示它.
|
3+5=8
7+9+11=27
13+15+17+19=64
21+23+25+27+25=125,
……
则这个式子为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com