
(1)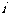 是虚数单位,
是虚数单位,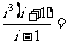
(A) 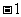 (B) 1 (C)
(B) 1 (C)  (D)
(D) 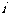
(2)设变量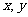 满足约束条件
满足约束条件 ,则目标函数
,则目标函数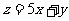 的最大值为
的最大值为
(A) 2 (B) 3 (C) 4 (D) 5
(3)设函数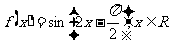 ,则
,则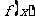 是
是
(A) 最小正周期为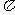 的奇函数 (B) 最小正周期为
的奇函数 (B) 最小正周期为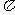 的偶函数
的偶函数
(C) 最小正周期为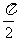 的奇函数 (D) 最小正周期为
的奇函数 (D) 最小正周期为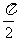 的偶函数
的偶函数
(4)设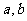 是两条直线,
是两条直线,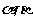 是两个平面,则
是两个平面,则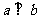 的一个充分条件是
的一个充分条件是
(A) 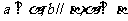 (B)
(B) 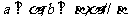
(C) 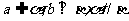 (D)
(D) 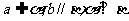
(5)设椭圆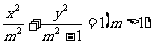 上一点P到其左焦点的距离为3,到右焦点的距离为1,则P到右准线的距离为
上一点P到其左焦点的距离为3,到右焦点的距离为1,则P到右准线的距离为
(A) 6 (B) 2 (C) 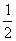 (D)
(D) 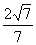
(6)设集合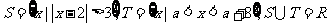 ,则
,则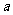 的取值范围是
的取值范围是
(A) 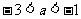 (B)
(B) 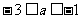
(C)  或
或 (D)
(D) 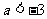 或
或
(7)设函数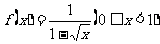 的反函数为
的反函数为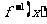 ,则
,则
(A) 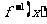 在其定义域上是增函数且最大值为1
在其定义域上是增函数且最大值为1
(B) 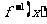 在其定义域上是减函数且最小值为0
在其定义域上是减函数且最小值为0
(C) 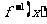 在其定义域上是减函数且最大值为1
在其定义域上是减函数且最大值为1
(D) 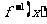 在其定义域上是增函数且最小值为0
在其定义域上是增函数且最小值为0
(8)已知函数 ,则不等式
,则不等式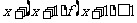 的解集是
的解集是
(A) 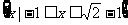 (B)
(B) 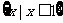
(C) 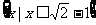 (D)
(D) 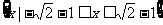
(9)已知函数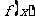 是定义在R上的偶函数,且在区间
是定义在R上的偶函数,且在区间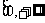 上是增函数.令
上是增函数.令
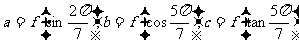 ,则
,则
(A) 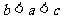 (B)
(B) 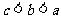 (C)
(C) 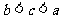 (D)
(D) 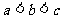
(10)有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有
(A) 1344种 (B) 1248种 (C) 1056种 (D) 960种
第Ⅱ卷
22.(本大题满分12分)
设函数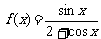
(Ⅰ)求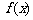 的单调区间;
的单调区间;
(Ⅱ)如果对任何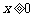 ,都有
,都有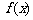
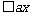 ,求
,求 的取值范围。
的取值范围。
21.(本大题满分12分)
设椭圆中心在坐标原点,A(2,0)、B(0,1)是它的两个顶点,直线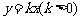 与AB相交于点D,与椭圆相交于E、F两点。
与AB相交于点D,与椭圆相交于E、F两点。
(Ⅰ)若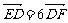 ,求
,求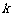 的值;
的值;
(Ⅱ)求四边形AEBF面积的最大值。
20.(本大题满分12分)
设数列{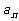 }的前
}的前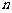 项和为S
项和为S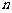 ,已知
,已知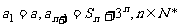
(Ⅰ)设bn=Sn-3n,求数列{bn}的通项公式;
(Ⅱ)若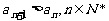 求
求 的取值范围。
的取值范围。
19.(本大题满分12分)
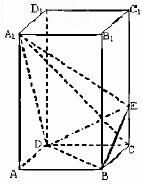
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC
(Ⅰ)证明:A1C⊥平面BED
(Ⅱ)求二面角A1-DE-B的大小
18.(本大题满分12分)
购买某种保险,每个投保人每年度向保险公司交纳保费a元,若投保人在购买保险的一年度内出险,则可以获得10000元的赔偿金,假定在一年度内有10000人购买了这种保险,且各投保人是否出险相互独立,已知保险公司在一年度内至少支付偿金10000元的概率为1―0.999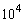
(Ⅰ)求一投保人在一年度内出险的概率p;
(Ⅱ)设保险公司开办该项险种业务除赔偿金外的成本为50000元,为保证盈利的期望不小于0,求每位投保人应交纳的最低保费(单位:元)
17.(本小题满分10分)
在△ABC中,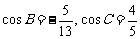
(Ⅰ)求sinA的值;
(Ⅱ)求△ABC的面积S△ABC=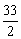 ,求BC的长。
,求BC的长。
16.平面内的一个四边形为平行四边形的充要条件有多个,如两组对边分别平行,类似地,写出空间中的一个四棱柱为平行六面体的两个充要条件:
充要条件:①______________________________;
充要条件:②______________________________
(写出你认为正确的两个充要条件)
15.已知F为抛物线C: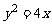 的焦点,过F且斜率为1的直线交于C于A、B两点。设|FA|>|FB|,则|FA|与|FB|的比值等于__________。
的焦点,过F且斜率为1的直线交于C于A、B两点。设|FA|>|FB|,则|FA|与|FB|的比值等于__________。
14.设曲线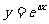 在点(0,1)处的切线与直线
在点(0,1)处的切线与直线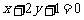 垂直,则
垂直,则 =__________。
=__________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com